Question and Answers Forum

AllQuestion and Answers: Page 311

Question Number 191149 Answers: 3 Comments: 3

The number of solutions of ∣x+3∣+∣x−2∣+3sinx−3=0 is

$${The}\:{number}\:{of}\:{solutions}\:{of} \\ $$$$\mid{x}+\mathrm{3}\mid+\mid{x}−\mathrm{2}\mid+\mathrm{3}{sinx}−\mathrm{3}=\mathrm{0}\:{is} \\ $$

Question Number 191148 Answers: 0 Comments: 0

Question Number 191147 Answers: 0 Comments: 0

Question Number 191146 Answers: 0 Comments: 0

Question Number 191144 Answers: 1 Comments: 0

Question Number 191143 Answers: 1 Comments: 0

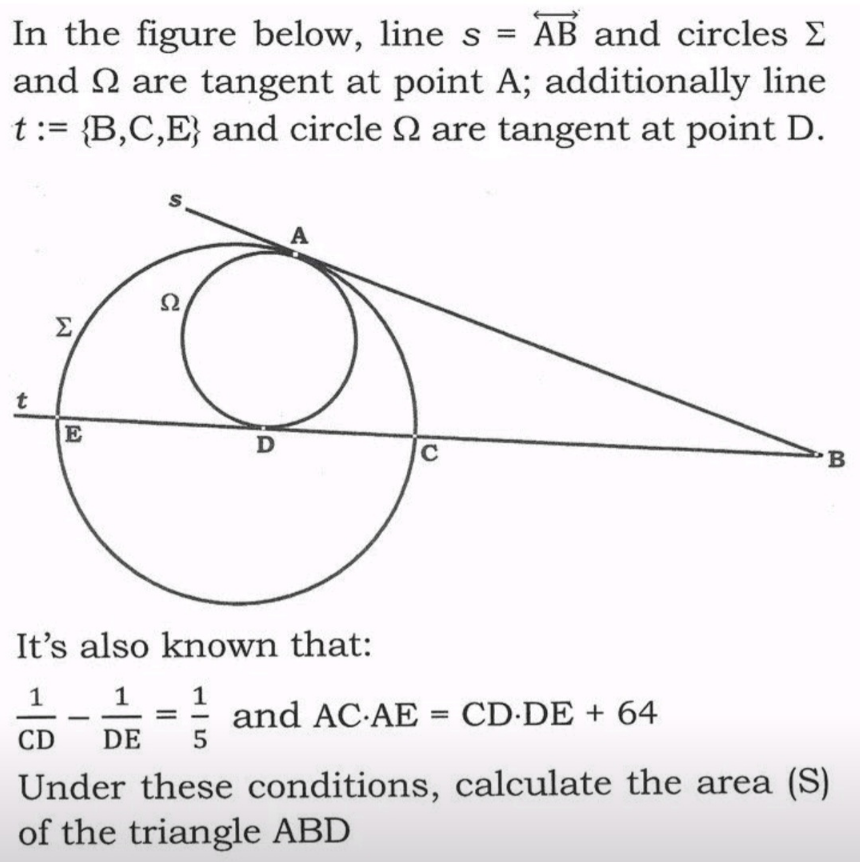
Question Number 191142 Answers: 0 Comments: 0

Question Number 191151 Answers: 1 Comments: 0

f(x)+f(1−x)=x^2 =>f(x)=¿

$${f}\left({x}\right)+{f}\left(\mathrm{1}−{x}\right)={x}^{\mathrm{2}} \\ $$$$=>{f}\left({x}\right)=¿ \\ $$

Question Number 191138 Answers: 0 Comments: 0

Question Number 191131 Answers: 2 Comments: 0

Question Number 191129 Answers: 2 Comments: 0

Solve for x : x + ln(1−x) = 0.1614 Help!

$$\mathrm{Solve}\:\mathrm{for}\:\mathrm{x}\:: \\ $$$$\mathrm{x}\:+\:\mathrm{ln}\left(\mathrm{1}−\mathrm{x}\right)\:=\:\mathrm{0}.\mathrm{1614} \\ $$$$ \\ $$$$\mathrm{Help}! \\ $$

Question Number 191128 Answers: 1 Comments: 0

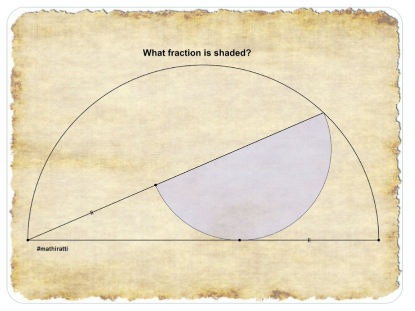
Question Number 191127 Answers: 0 Comments: 0

Question Number 191126 Answers: 0 Comments: 1

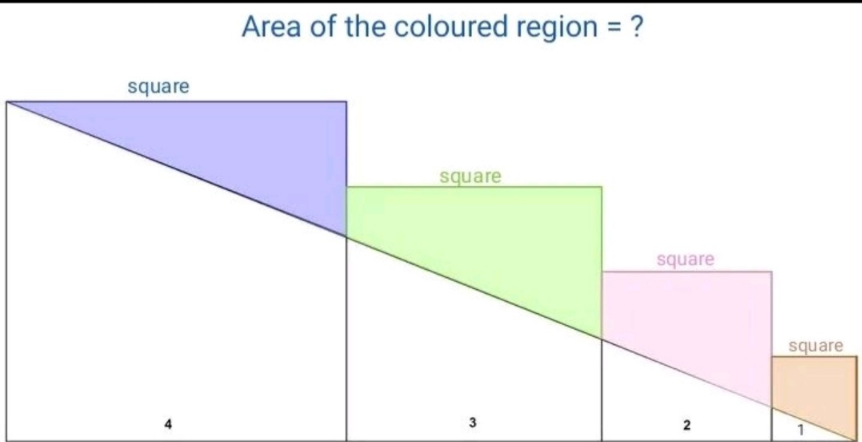
Question Number 191121 Answers: 0 Comments: 0

Question Number 191111 Answers: 0 Comments: 2

bb55bb

$${bb}\mathrm{55}{bb} \\ $$

Question Number 191104 Answers: 1 Comments: 0

Question Number 191103 Answers: 1 Comments: 0

Question Number 191102 Answers: 2 Comments: 0

Question Number 191091 Answers: 1 Comments: 0

The front of a train 80m long passes a signal at a speed of 72km/h. If the rear of the train passes the signal 5seconds later, find (a) the acceleration of the train (b) the speed at which the rear of the train passes the signal.

$${The}\:{front}\:{of}\:{a}\:{train}\:\mathrm{80}{m}\:{long}\:{passes} \\ $$$${a}\:{signal}\:{at}\:{a}\:{speed}\:{of}\:\mathrm{72}{km}/{h}.\:{If}\:{the} \\ $$$${rear}\:{of}\:{the}\:{train}\:{passes}\:{the}\:{signal}\: \\ $$$$\mathrm{5}{seconds}\:{later},\:{find}\: \\ $$$$\left({a}\right)\:{the}\:{acceleration}\:{of}\:{the}\:{train} \\ $$$$\left({b}\right)\:{the}\:{speed}\:{at}\:{which}\:{the}\:{rear}\:{of}\:{the} \\ $$$${train}\:{passes}\:{the}\:{signal}. \\ $$

Question Number 191078 Answers: 2 Comments: 0

lim_(x→0) ((x−sinx)/x^3 )=? solve without hopital and any series.

$$\underset{{x}\rightarrow\mathrm{0}} {\mathrm{lim}}\frac{{x}−{sinx}}{{x}^{\mathrm{3}} }=? \\ $$$${solve}\:{without}\:{hopital}\:{and}\:{any}\:{series}. \\ $$

Question Number 191077 Answers: 3 Comments: 2

a^→ ∙ b^(→) = 4 b^→ ∙ c^(→) = 5 7a^(→) = 4b^(→) + 2c^(→) Find: ∣c^(→) ∣ = ?

$$\overset{\rightarrow} {\mathrm{a}}\:\centerdot\:\overset{\rightarrow} {\mathrm{b}}\:=\:\mathrm{4} \\ $$$$\overset{\rightarrow} {\mathrm{b}}\:\centerdot\:\overset{\rightarrow} {\mathrm{c}}\:=\:\mathrm{5} \\ $$$$\overset{\rightarrow} {\mathrm{7a}}\:=\:\overset{\rightarrow} {\mathrm{4b}}\:+\:\overset{\rightarrow} {\mathrm{2c}}\:\: \\ $$$$\mathrm{Find}:\:\:\:\mid\overset{\rightarrow} {\mathrm{c}}\:\mid\:=\:? \\ $$

Question Number 191076 Answers: 1 Comments: 0

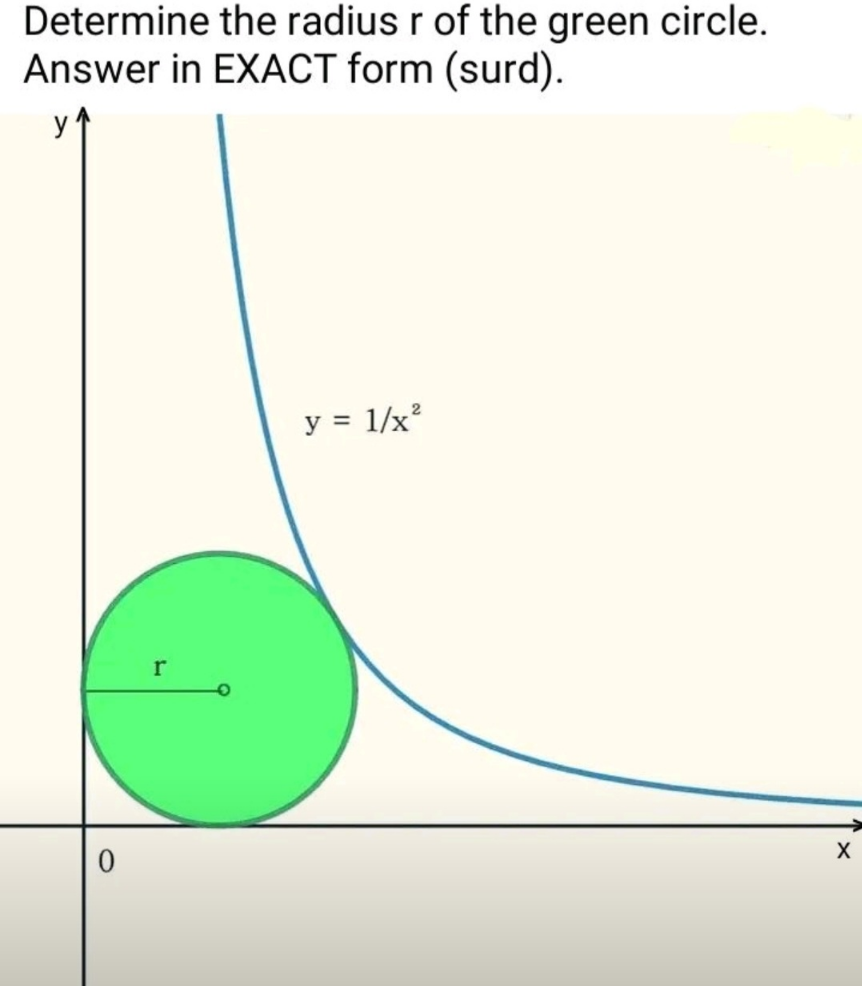
Question Number 191071 Answers: 0 Comments: 2

$$\: // \\ $$$$ \\ $$

Question Number 191069 Answers: 0 Comments: 1

both has same number of degrees, edges and vertices, i think the graph below are not isomorhic hos do i prove it?

$$ \\ $$$$\:{both}\:{has}\:{same}\:{number}\:{of}\:{degrees},\:{edges} \\ $$$$\:{and}\:{vertices},\:{i}\:{think}\:{the}\:{graph}\:{below}\:{are}\:{not} \\ $$$$\:{isomorhic}\:{hos}\:{do}\:{i}\:{prove}\:{it}? \\ $$$$ \\ $$

Question Number 191063 Answers: 0 Comments: 0

Pg 306 Pg 307 Pg 308 Pg 309 Pg 310 Pg 311 Pg 312 Pg 313 Pg 314 Pg 315

Contact: [email protected]