Question and Answers Forum

AllQuestion and Answers: Page 308

Question Number 190508 Answers: 3 Comments: 0

Question Number 190487 Answers: 1 Comments: 0

Question Number 190480 Answers: 1 Comments: 0

Proof that ((√2))^(√2) ∈R\Q

$$\mathrm{Proof}\:\mathrm{that}\:\left(\sqrt{\mathrm{2}}\right)^{\sqrt{\mathrm{2}}} \in\mathbb{R}\backslash\mathrm{Q} \\ $$

Question Number 190464 Answers: 1 Comments: 0

{ ((u_(n+1) = u_n −3 )),((v_(n+1) = 4v_n )) :} : u_0 = v_0 = 1 w_n = ((1−u_n )/v_n ) − show that w_n is bounded − find a,b∈R such that a ≤ w_n ≤ b

$$\begin{cases}{{u}_{{n}+\mathrm{1}} \:=\:{u}_{{n}} −\mathrm{3}\:}\\{{v}_{{n}+\mathrm{1}} \:=\:\mathrm{4}{v}_{{n}} }\end{cases}\::\:{u}_{\mathrm{0}} \:=\:{v}_{\mathrm{0}} \:=\:\mathrm{1} \\ $$$${w}_{{n}} \:=\:\frac{\mathrm{1}−{u}_{{n}} }{{v}_{{n}} } \\ $$$$−\:{show}\:{that}\:{w}_{{n}} \:{is}\:{bounded} \\ $$$$−\:{find}\:{a},{b}\in\mathbb{R}\:{such}\:{that}\:{a}\:\leqslant\:{w}_{{n}} \:\leqslant\:{b} \\ $$

Question Number 190452 Answers: 0 Comments: 0

∫((cos^(1.5) x−sin^(1.5) x)/( (√(sinx cosx)))) dx = ∫((cos^(3/2) x)/(sin^(1/2) x cos^(1/2) x))dx−∫((sin^(3/2) x)/(sin^(1/2) x cos^(1/2) x)) dx = ∫ ((cosx)/(sin^(1/2) x)) dx − ∫ ((sinx)/(cos^(1/2) x)) dx = ∫ (dt/t^(1/2) ) − ∫ (((−dz))/z^(1/2) ) where cosx = z and sinx = t = 2 (√(sinx)) + 2 (√(cosx)) + C

Question Number 190459 Answers: 1 Comments: 7

hi me tinko Tara Hello, when I use my mobile keyboard, the writing is on the right side, and when I use the math editor keyboard, the writing is still on the right side. I want the question to be typed on the left side, like

$$ \\ $$hi me tinko Tara Hello, when I use my mobile keyboard, the writing is on the right side, and when I use the math editor keyboard, the writing is still on the right side. I want the question to be typed on the left side, like

Question Number 190450 Answers: 0 Comments: 0

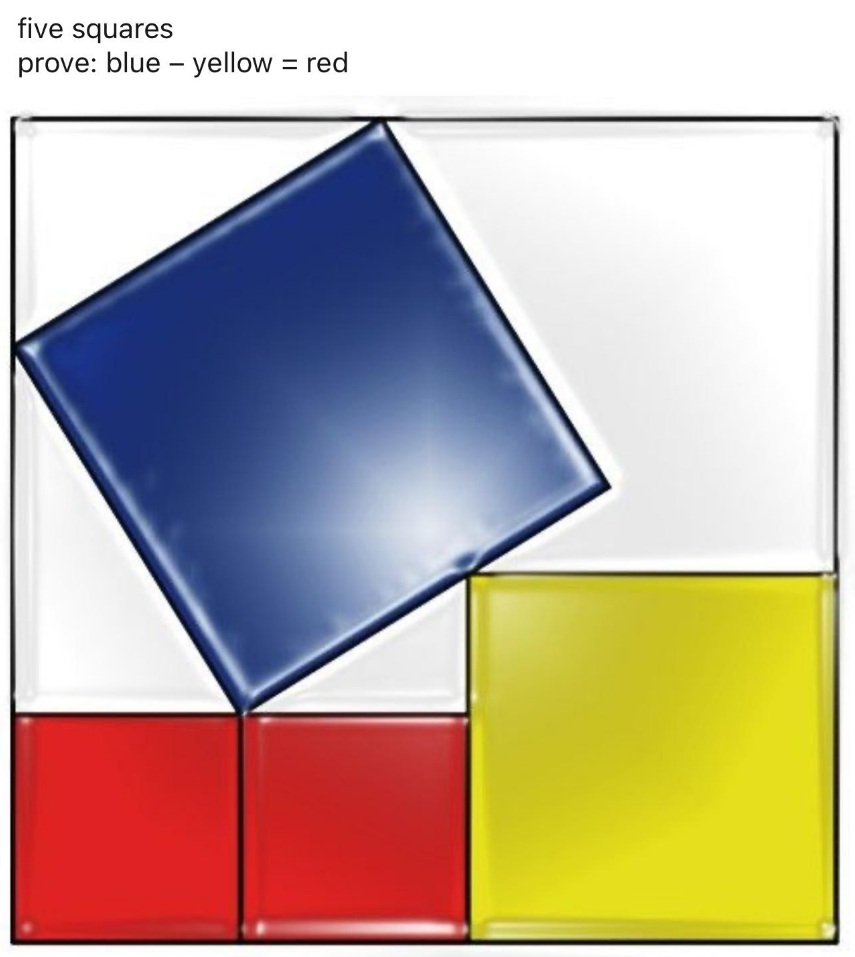
Question Number 190449 Answers: 1 Comments: 0

John stands at 10m from a mango tree while Philip stands between John and the Philip. The angle of elevation from John and Philip is 55º and 70º respectively. If John is 1.7m tall and Philip is 1.5m tall, find the minimum length of stick they will each need to touch the mango from their position. Help Please

$$ \\ $$John stands at 10m from a mango tree while Philip stands between John and the Philip. The angle of elevation from John and Philip is 55º and 70º respectively. If John is 1.7m tall and Philip is 1.5m tall, find the minimum length of stick they will each need to touch the mango from their position. Help Please

Question Number 190448 Answers: 1 Comments: 0

Question Number 190443 Answers: 0 Comments: 0

Question Number 190501 Answers: 1 Comments: 0

lim_(x→∞) (3^x /(x!))=? solution?

$$\underset{{x}\rightarrow\infty} {\mathrm{lim}}\frac{\mathrm{3}^{\mathrm{x}} }{\mathrm{x}!}=? \\ $$$$\mathrm{solution}? \\ $$

Question Number 190435 Answers: 2 Comments: 0

how is solution lim_(x→0) ((x^(10) ∙sin^4 x∙cos^8 x∙(x+1)^3 )/(x^4 +3x^3 +3x^2 +x))=?

$$ \\ $$$$\mathrm{how}\:\mathrm{is}\:\mathrm{solution} \\ $$$$\underset{{x}\rightarrow\mathrm{0}} {\mathrm{lim}}\frac{\mathrm{x}^{\mathrm{10}} \centerdot\mathrm{sin}^{\mathrm{4}} \mathrm{x}\centerdot\mathrm{cos}^{\mathrm{8}} \mathrm{x}\centerdot\left(\mathrm{x}+\mathrm{1}\right)^{\mathrm{3}} }{\mathrm{x}^{\mathrm{4}} +\mathrm{3x}^{\mathrm{3}} +\mathrm{3x}^{\mathrm{2}} +\mathrm{x}}=? \\ $$$$ \\ $$

Question Number 190425 Answers: 1 Comments: 0

Question Number 190420 Answers: 1 Comments: 2

laplace transform −−−−−−− L_t { (( sin(t ))/t) } = F (s ) F (s )= ? then calculate . Ω=∫_0 ^( ∞) ((e^( −2t) sin(t ))/t) dt =? −−−−−−−−

$$\:\:\:\:\:\:\:\:\:\:\:\:\:\:\mathrm{laplace}\:\:\mathrm{transform} \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:\:−−−−−−− \\ $$$$\:\:\:\:\:\:\:\:\:\:\mathcal{L}_{{t}} \:\left\{\:\:\frac{\:\mathrm{sin}\left({t}\:\right)}{{t}}\:\:\right\}\:=\:\mathcal{F}\:\left({s}\:\right)\:\:\:\:\:\:\:\:\:\:\: \\ $$$$\:\: \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\mathcal{F}\:\left({s}\:\right)=\:\:?\:\: \\ $$$$ \\ $$$$\:\:\:\:\:\:\:\:\:{then}\:\:{calculate}\:. \\ $$$$ \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:\Omega=\int_{\mathrm{0}} ^{\:\infty} \frac{{e}^{\:−\mathrm{2}{t}} {sin}\left({t}\:\right)}{{t}}\:{dt}\:=? \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:−−−−−−−− \\ $$

Question Number 190419 Answers: 1 Comments: 0

∫_(−1) ^1 ∫_(−(√(1−y^2 ))) ^(√(1−y^2 )) ln (x^2 +y^2 +1)dx dy =?

$$\:\underset{−\mathrm{1}} {\overset{\mathrm{1}} {\int}}\underset{−\sqrt{\mathrm{1}−{y}^{\mathrm{2}} }} {\overset{\sqrt{\mathrm{1}−{y}^{\mathrm{2}} }} {\int}}\:\mathrm{ln}\:\left({x}^{\mathrm{2}} +{y}^{\mathrm{2}} +\mathrm{1}\right){dx}\:{dy}\:=? \\ $$

Question Number 190407 Answers: 2 Comments: 0

Question Number 190405 Answers: 5 Comments: 0

Question Number 190402 Answers: 0 Comments: 6

v2.272 fixes some issues with cursor position while writing Right to Left Languages (such as arabic) using system keyboard.

$$\mathrm{v2}.\mathrm{272}\:\mathrm{fixes}\:\mathrm{some}\:\mathrm{issues}\:\mathrm{with}\:\mathrm{cursor} \\ $$$$\mathrm{position}\:\mathrm{while}\:\mathrm{writing}\:\mathrm{Right}\:\mathrm{to}\:\mathrm{Left} \\ $$$$\mathrm{Languages}\:\left(\mathrm{such}\:\mathrm{as}\:\mathrm{arabic}\right)\:\mathrm{using} \\ $$$$\mathrm{system}\:\mathrm{keyboard}. \\ $$

Question Number 190401 Answers: 1 Comments: 0

Determine the validity of the following argument. Having nasal congestion is not sufficient to be diagnosed of Covid−19 disease. Being accinated against covid−19 is necessary for not being diagnosed of covid−19. Therefore,if i′m diagnosed of covid−19 then it is not the case that either I have not vaccinated against covid−19 or I have nasal congestion.

$$\mathrm{Determine}\:\mathrm{the}\:\mathrm{validity}\:\mathrm{of}\:\mathrm{the}\:\mathrm{following}\:\mathrm{argument}. \\ $$$$\mathrm{Having}\:\mathrm{nasal}\:\mathrm{congestion}\:\mathrm{is}\:\mathrm{not}\:\mathrm{sufficient}\:\mathrm{to}\:\mathrm{be} \\ $$$$\mathrm{diagnosed}\:\mathrm{of}\:\mathrm{Covid}−\mathrm{19}\:\mathrm{disease}. \\ $$$$\mathrm{Being}\:\mathrm{accinated}\:\mathrm{against}\:\mathrm{covid}−\mathrm{19}\:\mathrm{is}\: \\ $$$$\mathrm{necessary}\:\mathrm{for}\:\mathrm{not}\:\mathrm{being}\:\mathrm{diagnosed} \\ $$$$\mathrm{of}\:\mathrm{covid}−\mathrm{19}.\:\mathrm{Therefore},\mathrm{if}\:\mathrm{i}'\mathrm{m}\:\mathrm{diagnosed} \\ $$$$\mathrm{of}\:\mathrm{covid}−\mathrm{19}\:\mathrm{then}\:\:\mathrm{it}\:\mathrm{is}\:\mathrm{not}\:\mathrm{the}\:\mathrm{case}\:\mathrm{that} \\ $$$$\mathrm{either}\:\mathrm{I}\:\mathrm{have}\:\mathrm{not}\:\mathrm{vaccinated}\:\mathrm{against}\:\mathrm{covid}−\mathrm{19} \\ $$$$\mathrm{or}\:\mathrm{I}\:\mathrm{have}\:\mathrm{nasal}\:\mathrm{congestion}. \\ $$

Question Number 190397 Answers: 1 Comments: 0

Question Number 190395 Answers: 3 Comments: 0

which is larger, 2^(234) or 5^(100) ?

$${which}\:{is}\:{larger}, \\ $$$$\mathrm{2}^{\mathrm{234}} \:{or}\:\mathrm{5}^{\mathrm{100}} \:? \\ $$

Question Number 190392 Answers: 1 Comments: 1

If a + b = 3 Find: ((a^2 + b^2 − 2a − 2b)/(a^2 − b^2 − 4a + 4))

$$\mathrm{If}\:\:\:\mathrm{a}\:+\:\mathrm{b}\:=\:\mathrm{3} \\ $$$$\mathrm{Find}:\:\:\:\frac{\mathrm{a}^{\mathrm{2}} \:+\:\mathrm{b}^{\mathrm{2}} \:−\:\mathrm{2a}\:−\:\mathrm{2b}}{\mathrm{a}^{\mathrm{2}} \:−\:\mathrm{b}^{\mathrm{2}} \:−\:\mathrm{4a}\:+\:\mathrm{4}} \\ $$

Question Number 190388 Answers: 0 Comments: 0

Question Number 190385 Answers: 1 Comments: 0

Question Number 190371 Answers: 1 Comments: 0

Question Number 190370 Answers: 1 Comments: 0

Pg 303 Pg 304 Pg 305 Pg 306 Pg 307 Pg 308 Pg 309 Pg 310 Pg 311 Pg 312

Contact: info@tinkutara.com