Question and Answers Forum

All Questions Topic List

AllQuestion and Answers: Page 278

Question Number 193391 Answers: 2 Comments: 0

Question Number 193390 Answers: 0 Comments: 0

A ship X sailing with a velocity (21 kmh 052⁰) observes a light from a lighthuse due North. The bearing of the liglhthouse from the ship 20 minutes later is found to be 312. calcuate correct to thre sigificant figures i) the orignal distance when the lighthoues is due West of the ship from the time when it is due North of the ship. ii) the time in minutes, when the lighthouse is due West of the ship from the time when it is due North of the ship. iii) the distance in km of the ship from then lighthoue when the lighthouse is due West of the ship

$$ \\ $$A ship X sailing with a velocity (21 kmh 052⁰) observes a light from a lighthuse due North. The bearing of the liglhthouse from the ship 20 minutes later is found to be 312. calcuate correct to thre sigificant figures i) the orignal distance when the lighthoues is due West of the ship from the time when it is due North of the ship. ii) the time in minutes, when the lighthouse is due West of the ship from the time when it is due North of the ship. iii) the distance in km of the ship from then lighthoue when the lighthouse is due West of the ship

Question Number 193389 Answers: 0 Comments: 0

Question Number 193387 Answers: 0 Comments: 1

Question Number 193385 Answers: 1 Comments: 0

Question Number 193381 Answers: 1 Comments: 0

Question Number 193377 Answers: 1 Comments: 1

Evaluate I=∫_0 ^( ∞) (1/(x^5 +x^4 +x^3 +x^2 +x+1))dx

$${Evaluate} \\ $$$${I}=\int_{\mathrm{0}} ^{\:\infty} \frac{\mathrm{1}}{{x}^{\mathrm{5}} +{x}^{\mathrm{4}} +{x}^{\mathrm{3}} +{x}^{\mathrm{2}} +{x}+\mathrm{1}}{dx} \\ $$

Question Number 193375 Answers: 0 Comments: 0

Quantitative Reasoning Example: P_4 +M_3 =16 M_4 −P_3 =18, P_5 +M_3 =2 Find: P_6 +M_4 =? P_5 −M_8 =? M_3 +M_2 =? M_5 −P_(10) =?

$${Quantitative}\:{Reasoning} \\ $$$${Example}:\:\:{P}_{\mathrm{4}} +{M}_{\mathrm{3}} =\mathrm{16} \\ $$$${M}_{\mathrm{4}} −{P}_{\mathrm{3}} =\mathrm{18},\:{P}_{\mathrm{5}} +{M}_{\mathrm{3}} =\mathrm{2} \\ $$$${Find}: \\ $$$${P}_{\mathrm{6}} +{M}_{\mathrm{4}} =? \\ $$$${P}_{\mathrm{5}} −{M}_{\mathrm{8}} =? \\ $$$${M}_{\mathrm{3}} +{M}_{\mathrm{2}} =? \\ $$$${M}_{\mathrm{5}} −{P}_{\mathrm{10}} =? \\ $$$$ \\ $$

Question Number 193371 Answers: 3 Comments: 0

Reduce to first order and solve , showing each step in detail. 1. y′′ +(y′)^3 siny=0 2. y′′=1+(y′)^2

$$\mathrm{Reduce}\:\mathrm{to}\:\mathrm{first}\:\mathrm{order}\:\mathrm{and}\:\mathrm{solve}\:, \\ $$$$\mathrm{showing}\:\mathrm{each}\:\mathrm{step}\:\mathrm{in}\:\mathrm{detail}. \\ $$$$\mathrm{1}.\:\mathrm{y}''\:+\left(\mathrm{y}'\right)^{\mathrm{3}} \mathrm{siny}=\mathrm{0} \\ $$$$\mathrm{2}.\:\mathrm{y}''=\mathrm{1}+\left(\mathrm{y}'\right)^{\mathrm{2}} \\ $$$$ \\ $$

Question Number 193368 Answers: 2 Comments: 0

If log_a y = (1/3) and log_8 a = x + 1 then show that y = 2^(x + 1)

$$\mathrm{If}\:\mathrm{log}_{{a}} {y}\:=\:\frac{\mathrm{1}}{\mathrm{3}}\:\mathrm{and}\:\mathrm{log}_{\mathrm{8}} {a}\:=\:{x}\:+\:\mathrm{1}\:\mathrm{then}\:\mathrm{show} \\ $$$$\mathrm{that}\:{y}\:=\:\mathrm{2}^{{x}\:+\:\mathrm{1}} \\ $$

Question Number 193366 Answers: 1 Comments: 0

2sin^2 2x>3cos x+3

$$\mathrm{2sin}\:^{\mathrm{2}} \mathrm{2}{x}>\mathrm{3cos}\:{x}+\mathrm{3} \\ $$

Question Number 193363 Answers: 1 Comments: 0

y = 4 × 10^(2x) Express x in terms of y, giving an exact simplified answer in terms of log base 10.

$${y}\:=\:\mathrm{4}\:×\:\mathrm{10}^{\mathrm{2}{x}} \\ $$$$\mathrm{Express}\:{x}\:\mathrm{in}\:\mathrm{terms}\:\mathrm{of}\:{y},\:\mathrm{giving}\:\mathrm{an}\:\mathrm{exact} \\ $$$$\mathrm{simplified}\:\mathrm{answer}\:\mathrm{in}\:\mathrm{terms}\:\mathrm{of}\:\mathrm{log}\:\mathrm{base}\:\mathrm{10}. \\ $$

Question Number 193360 Answers: 2 Comments: 0

If x = 2^p and y = 4^q then prove that log_2 (x^3 y) = 3p + 2q

$$\mathrm{If}\:{x}\:=\:\mathrm{2}^{{p}} \:\mathrm{and}\:{y}\:=\:\mathrm{4}^{{q}} \:\mathrm{then}\:\mathrm{prove}\:\mathrm{that} \\ $$$$\mathrm{log}_{\mathrm{2}} \left({x}^{\mathrm{3}} {y}\right)\:=\:\mathrm{3}{p}\:+\:\mathrm{2}{q} \\ $$

Question Number 193356 Answers: 2 Comments: 0

Question Number 193351 Answers: 0 Comments: 0

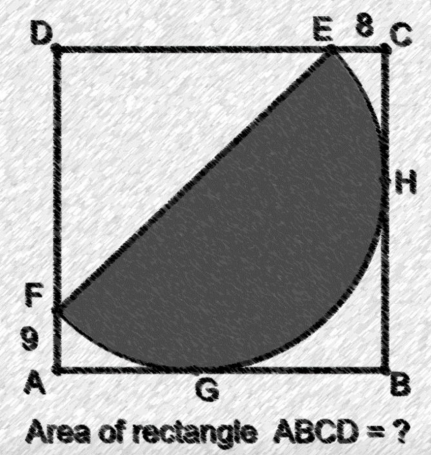
Question Number 193350 Answers: 0 Comments: 0

Question Number 193349 Answers: 1 Comments: 0

Question Number 193346 Answers: 2 Comments: 0

(√(4x−3))−(√(2x−5))=2 solve for x

$$\sqrt{\mathrm{4x}−\mathrm{3}}−\sqrt{\mathrm{2x}−\mathrm{5}}=\mathrm{2} \\ $$$$\mathrm{solve}\:\mathrm{for}\:\mathrm{x} \\ $$

Question Number 193345 Answers: 1 Comments: 0

Question Number 193336 Answers: 1 Comments: 1

Question Number 193333 Answers: 0 Comments: 1

Question Number 193332 Answers: 0 Comments: 0

Question Number 193331 Answers: 0 Comments: 0

Question Number 193328 Answers: 1 Comments: 0

f(x)= { ((((x^2 −x)/(x^2 −1)) ; x≠1)),((2x+1; x=1)) :} thene find lim_(x→1) f(x)=?

$$\mathrm{f}\left(\mathrm{x}\right)=\begin{cases}{\frac{\mathrm{x}^{\mathrm{2}} −\mathrm{x}}{\mathrm{x}^{\mathrm{2}} −\mathrm{1}}\:;\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\mathrm{x}\neq\mathrm{1}}\\{\mathrm{2x}+\mathrm{1};\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\mathrm{x}=\mathrm{1}}\end{cases} \\ $$$$\mathrm{thene}\:\mathrm{find}\:\underset{{x}\rightarrow\mathrm{1}} {\mathrm{lim}}{f}\left({x}\right)=? \\ $$

Question Number 193329 Answers: 0 Comments: 0

Question Number 193323 Answers: 1 Comments: 0

Pg 273 Pg 274 Pg 275 Pg 276 Pg 277 Pg 278 Pg 279 Pg 280 Pg 281 Pg 282

Terms of Service

Contact: info@tinkutara.com