
AllQuestion and Answers: Page 269
Question Number 195555 Answers: 1 Comments: 0

Question Number 195554 Answers: 0 Comments: 0

Question Number 195553 Answers: 1 Comments: 0

Question Number 195301 Answers: 1 Comments: 0
Question Number 195292 Answers: 1 Comments: 0

Question Number 195291 Answers: 1 Comments: 0
Question Number 195288 Answers: 0 Comments: 1
Question Number 195287 Answers: 2 Comments: 0

Question Number 200309 Answers: 2 Comments: 0

Question Number 195289 Answers: 1 Comments: 0

Question Number 195290 Answers: 1 Comments: 0
Question Number 195322 Answers: 1 Comments: 0
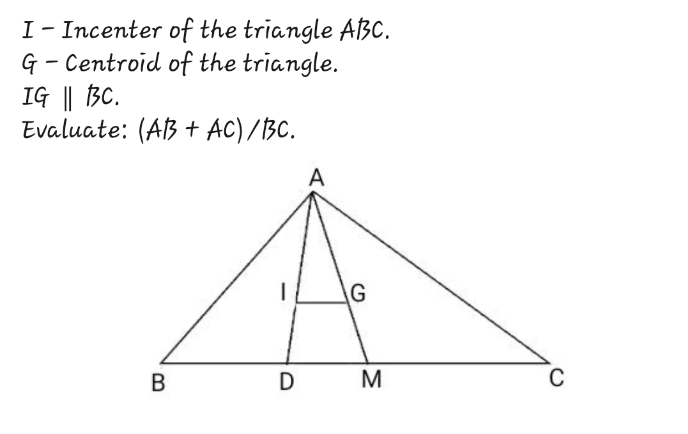
Question Number 200300 Answers: 1 Comments: 0

Question Number 200299 Answers: 1 Comments: 0

Question Number 200298 Answers: 1 Comments: 1

Question Number 195273 Answers: 0 Comments: 1

Question Number 195454 Answers: 4 Comments: 1

Question Number 195453 Answers: 1 Comments: 1
Question Number 195263 Answers: 2 Comments: 0
Question Number 195259 Answers: 0 Comments: 1
Question Number 195255 Answers: 2 Comments: 0
$$\int\frac{{dx}}{\mathrm{cos}\:^{\mathrm{3}} {x}\sqrt{\mathrm{4sin}\:{x}\mathrm{cos}\:{x}}} \\ $$
Question Number 195254 Answers: 1 Comments: 0
Question Number 195253 Answers: 2 Comments: 1
Question Number 195252 Answers: 1 Comments: 0
Question Number 195251 Answers: 0 Comments: 1
Question Number 195248 Answers: 0 Comments: 3

Pg 264 Pg 265 Pg 266 Pg 267 Pg 268 Pg 269 Pg 270 Pg 271 Pg 272 Pg 273
