
AllQuestion and Answers: Page 268
Question Number 195064 Answers: 0 Comments: 0

Question Number 195046 Answers: 2 Comments: 1

Question Number 195043 Answers: 2 Comments: 1

Question Number 195042 Answers: 1 Comments: 0

Question Number 195038 Answers: 0 Comments: 1
Question Number 195035 Answers: 2 Comments: 0
Question Number 195033 Answers: 1 Comments: 0
Question Number 195029 Answers: 1 Comments: 0
Question Number 195027 Answers: 1 Comments: 2
Question Number 195021 Answers: 1 Comments: 0
Question Number 195020 Answers: 1 Comments: 0
$${y}={x}^{{x}^{{x}...} } \\ $$$$=>\:\frac{{dy}}{{dx}}=¿ \\ $$
Question Number 195017 Answers: 3 Comments: 0
$$\left({x}+\mathrm{1}\right)^{\mathrm{3}} =\mathrm{1}\:\:\:\:\:\:\:\:\:\:{x}=? \\ $$
Question Number 195015 Answers: 1 Comments: 0
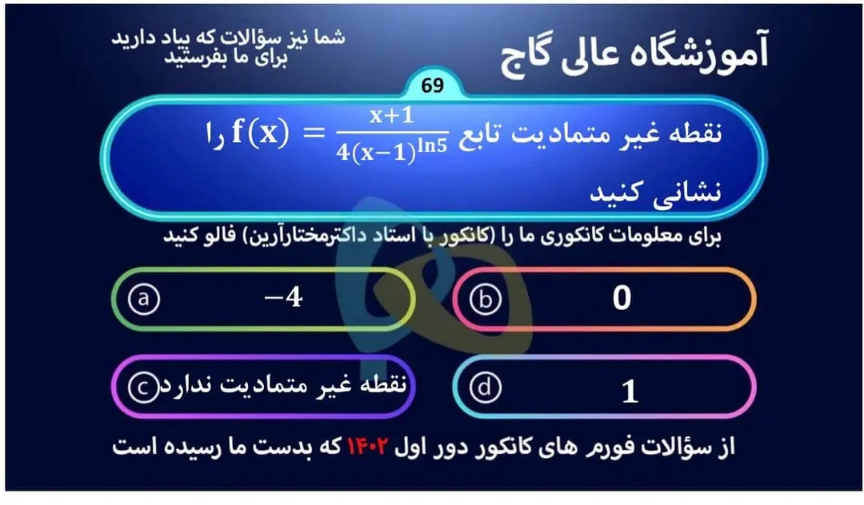
Question Number 195013 Answers: 1 Comments: 0
Question Number 195012 Answers: 2 Comments: 0

Question Number 195003 Answers: 1 Comments: 0
Question Number 195002 Answers: 1 Comments: 0
$${x}^{\sqrt{{x}}} =\left(\sqrt{{x}}\right)^{{x}} \:\:\:\:\:{x}=? \\ $$
Question Number 194998 Answers: 0 Comments: 2
Question Number 194985 Answers: 0 Comments: 0
Question Number 194991 Answers: 0 Comments: 4
Question Number 194990 Answers: 0 Comments: 0
Question Number 194988 Answers: 1 Comments: 0
Question Number 194971 Answers: 1 Comments: 2

Question Number 194968 Answers: 2 Comments: 0

Question Number 194967 Answers: 1 Comments: 0
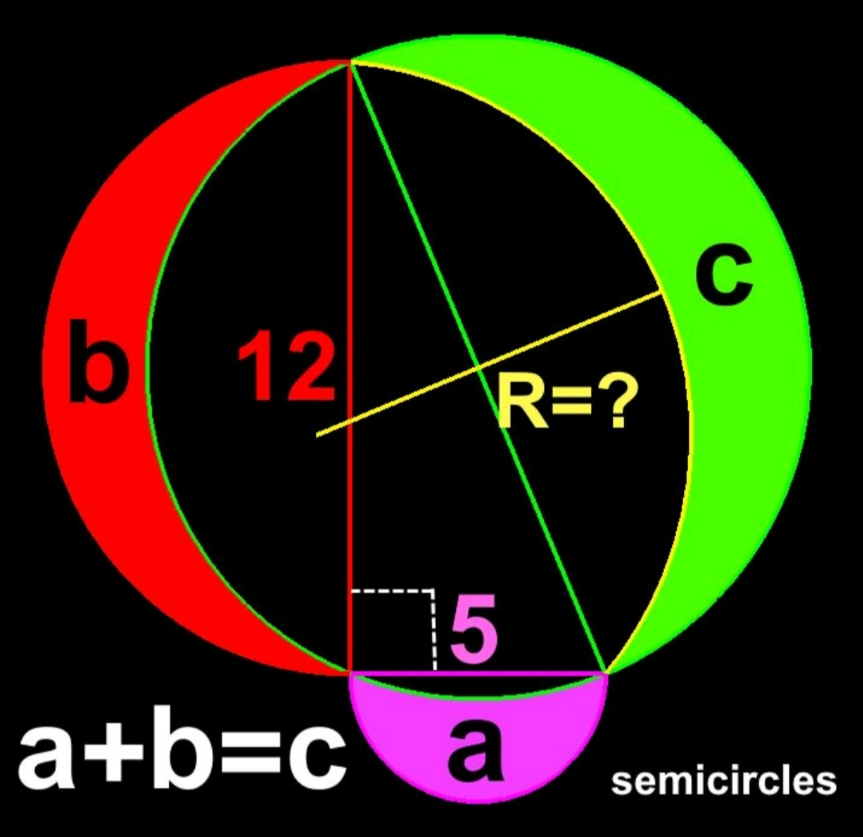
Question Number 194963 Answers: 2 Comments: 0

Pg 263 Pg 264 Pg 265 Pg 266 Pg 267 Pg 268 Pg 269 Pg 270 Pg 271 Pg 272
