Question and Answers Forum

All Questions Topic List

AllQuestion and Answers: Page 257

Question Number 195555 Answers: 1 Comments: 0

Question Number 195554 Answers: 0 Comments: 0

Question Number 195553 Answers: 1 Comments: 0

Question Number 195301 Answers: 1 Comments: 0

{ ((x^2 +y=11)),((x+y^2 =7)) :}⇒ x,y=?

$$\begin{cases}{{x}^{\mathrm{2}} +{y}=\mathrm{11}}\\{{x}+{y}^{\mathrm{2}} =\mathrm{7}}\end{cases}\Rightarrow\:{x},{y}=? \\ $$

Question Number 195292 Answers: 1 Comments: 0

Question Number 195291 Answers: 1 Comments: 0

it is given a,b,c ∈ N^∗ and ab<c . Prove that a+b≤c.

$$\:\:{it}\:{is}\:{given}\:{a},{b},{c}\:\in\:\mathbb{N}^{\ast} \:\:{and}\:\:{ab}<{c}\:.\:{Prove}\:{that}\:{a}+{b}\leqslant{c}. \\ $$

Question Number 195288 Answers: 0 Comments: 1

x, y, z∈R_+ , P = (x/(x + y)) + (y/(y + z)) + (z/(z + x)), Q = (y/(x + y)) + (z/(y + z)) + (x/(z + x)), Q = (z/(x + y)) + (x/(y + z)) + (y/(z + x)). f(x, y, z)=max{P, Q, R}, find f_(min) .

$${x},\:{y},\:{z}\in\mathbb{R}_{+} , \\ $$$${P}\:=\:\frac{{x}}{{x}\:+\:{y}}\:+\:\frac{{y}}{{y}\:+\:{z}}\:+\:\frac{{z}}{{z}\:+\:{x}}, \\ $$$${Q}\:=\:\frac{{y}}{{x}\:+\:{y}}\:+\:\frac{{z}}{{y}\:+\:{z}}\:+\:\frac{{x}}{{z}\:+\:{x}}, \\ $$$${Q}\:=\:\frac{{z}}{{x}\:+\:{y}}\:+\:\frac{{x}}{{y}\:+\:{z}}\:+\:\frac{{y}}{{z}\:+\:{x}}. \\ $$$${f}\left({x},\:{y},\:{z}\right)=\mathrm{max}\left\{{P},\:{Q},\:{R}\right\},\:\mathrm{find}\:{f}_{\mathrm{min}} . \\ $$

Question Number 195287 Answers: 2 Comments: 0

Question Number 200309 Answers: 2 Comments: 0

Question Number 195289 Answers: 1 Comments: 0

Question Number 195290 Answers: 1 Comments: 0

A professor said 0∣0 because 0= 0×a+0 , a∈ N. Can you prove?

$$\:{A}\:{professor}\:{said}\:\:\mathrm{0}\mid\mathrm{0}\:{because}\:\mathrm{0}=\:\mathrm{0}×{a}+\mathrm{0}\:\:\:,\:{a}\in\:\mathbb{N}.\:{Can}\:{you}\:{prove}? \\ $$

Question Number 195322 Answers: 1 Comments: 0

Question Number 200300 Answers: 1 Comments: 0

Question Number 200299 Answers: 1 Comments: 0

Question Number 200298 Answers: 1 Comments: 1

Question Number 195273 Answers: 0 Comments: 1

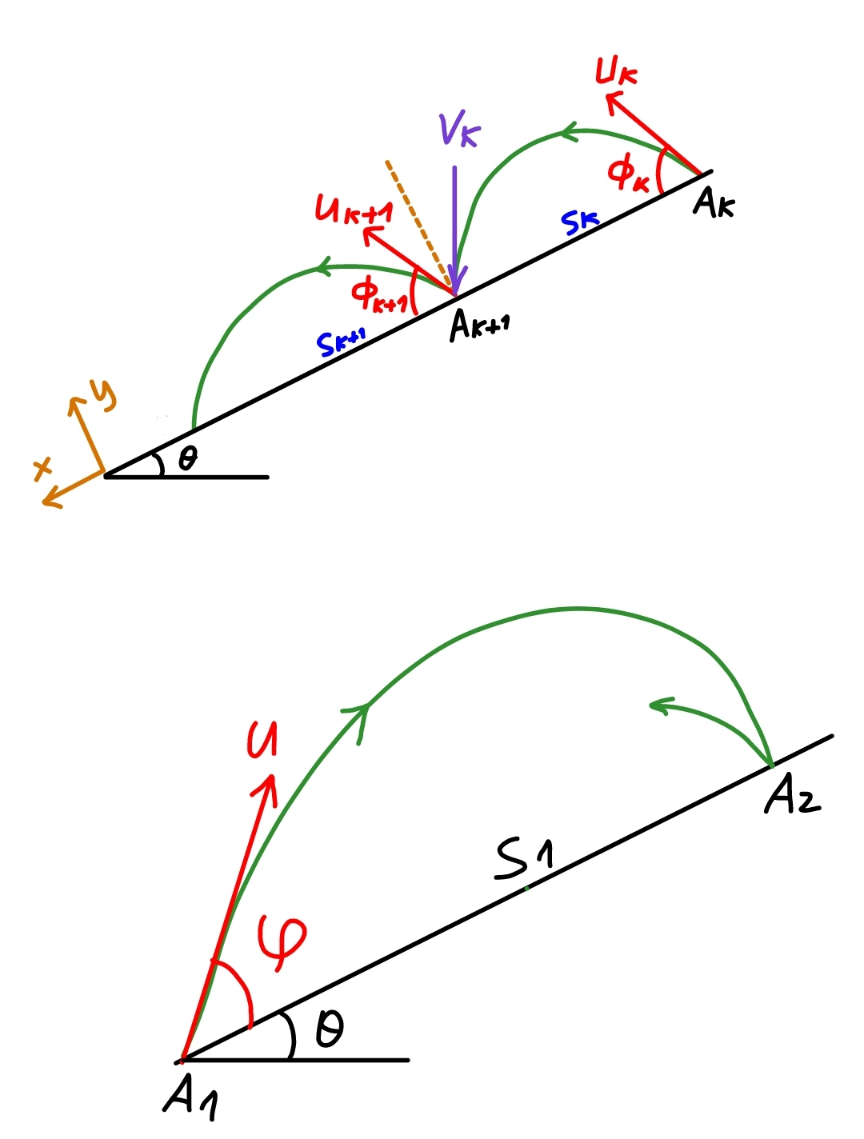
Question Number 195454 Answers: 4 Comments: 1

Question Number 195453 Answers: 1 Comments: 1

lim_(x→+∞ ) x ln(((e^x + 1)/(e^x −1))) ?

$$\:\:\:\:\mathrm{lim}_{{x}\rightarrow+\infty\:\:} \:{x}\:{ln}\left(\frac{{e}^{{x}} +\:\mathrm{1}}{{e}^{{x}} −\mathrm{1}}\right)\:\:? \\ $$

Question Number 195263 Answers: 2 Comments: 0

{ ((y sin x+cos x = 2)),((4sin x−2y cos x = y)) :} tan x =?

$$\:\:\:\:\:\:\begin{cases}{{y}\:\mathrm{sin}\:{x}+\mathrm{cos}\:{x}\:=\:\mathrm{2}}\\{\mathrm{4sin}\:{x}−\mathrm{2}{y}\:\mathrm{cos}\:{x}\:=\:{y}}\end{cases} \\ $$$$\:\:\:\:\:\:\:\mathrm{tan}\:{x}\:=?\: \\ $$

Question Number 195259 Answers: 0 Comments: 1

prove that lim_(n→∞) ((e^n ∙(n!))/(n^n (√n)))=(√(2π))

$${prove}\:{that} \\ $$$$\underset{{n}\rightarrow\infty} {\mathrm{lim}}\:\frac{{e}^{{n}} \centerdot\left({n}!\right)}{{n}^{{n}} \:\sqrt{{n}}}=\sqrt{\mathrm{2}\pi} \\ $$

Question Number 195255 Answers: 2 Comments: 0

∫(dx/(cos^3 x(√(4sin xcos x))))

$$\int\frac{{dx}}{\mathrm{cos}\:^{\mathrm{3}} {x}\sqrt{\mathrm{4sin}\:{x}\mathrm{cos}\:{x}}} \\ $$

Question Number 195254 Answers: 1 Comments: 0

∫^(spillover) ((sin^2 xcos^2 x)/((sin^5 x+cos^3 xsin^2 x+sin^3 xcos^2 x+cos^5 x)^2 ))dx

$$\int^{\boldsymbol{{spillover}}} \frac{\mathrm{sin}\:^{\mathrm{2}} {x}\mathrm{cos}\:^{\mathrm{2}} {x}}{\left(\mathrm{sin}\:^{\mathrm{5}} {x}+\mathrm{cos}\:^{\mathrm{3}} {x}\mathrm{sin}\:^{\mathrm{2}} {x}+\mathrm{sin}\:^{\mathrm{3}} {x}\mathrm{cos}\:^{\mathrm{2}} {x}+\mathrm{cos}\:^{\mathrm{5}} {x}\right)^{\mathrm{2}} }{dx} \\ $$

Question Number 195253 Answers: 2 Comments: 1

If 10sin^4 x+15cos^4 x=6. find the value of 27cosec^6 x+8sec^6 x

$${If}\:\mathrm{10sin}\:^{\mathrm{4}} {x}+\mathrm{15cos}\:^{\mathrm{4}} {x}=\mathrm{6}. \\ $$$${find}\:{the}\:{value}\:{of} \\ $$$$\mathrm{27cosec}\:^{\mathrm{6}} {x}+\mathrm{8sec}\:^{\mathrm{6}} {x} \\ $$$$ \\ $$

Question Number 195252 Answers: 1 Comments: 0

∫_(spillover) (dx/( (√e^(5x) ) (√((e^(2x) +e^(−2x) )^3 ))))

$$\int_{\boldsymbol{{spillover}}} \:\:\:\:\:\:\frac{{dx}}{\:\sqrt{{e}^{\mathrm{5}{x}} }\:\sqrt{\left({e}^{\mathrm{2}{x}} +{e}^{−\mathrm{2}{x}} \right)^{\mathrm{3}} }} \\ $$

Question Number 195251 Answers: 0 Comments: 1

If x^([16(log _5 x)^3 −68log _5 x]) =5^(−16) then Find the the product of x

$${If}\:\:{x}^{\left[\mathrm{16}\left(\mathrm{log}\:_{\mathrm{5}} {x}\right)^{\mathrm{3}} −\mathrm{68log}\:_{\mathrm{5}} {x}\right]} =\mathrm{5}^{−\mathrm{16}} \: \\ $$$$\:{then}\:{Find}\:{the}\:{the}\:{product}\:{of}\:{x} \\ $$$$ \\ $$

Question Number 195248 Answers: 0 Comments: 3

Pg 252 Pg 253 Pg 254 Pg 255 Pg 256 Pg 257 Pg 258 Pg 259 Pg 260 Pg 261

Contact: info@tinkutara.com