Question and Answers Forum

AllQuestion and Answers: Page 245

Question Number 197461 Answers: 1 Comments: 0

Prove that: •∫^( x) _( 0) ((lnt)/(t^2 −1))dt=∫^( (π/2)) _( 0) arctan(xtanθ)dθ • ∫^( x) _( (1/x)) ((lnt)/(t^2 −1))arctant dt=(π/8)∫^( π) _( 0) arctan((1/2)(x−(1/x))sint)dt

$$\mathrm{Prove}\:\mathrm{that}: \\ $$$$\bullet\underset{\:\mathrm{0}} {\int}^{\:\mathrm{x}} \frac{\mathrm{lnt}}{\mathrm{t}^{\mathrm{2}} −\mathrm{1}}\mathrm{dt}=\underset{\:\mathrm{0}} {\int}^{\:\frac{\pi}{\mathrm{2}}} \mathrm{arctan}\left(\mathrm{xtan}\theta\right)\mathrm{d}\theta \\ $$$$\bullet\:\:\underset{\:\frac{\mathrm{1}}{\mathrm{x}}} {\int}^{\:\mathrm{x}} \frac{\mathrm{lnt}}{\mathrm{t}^{\mathrm{2}} −\mathrm{1}}\mathrm{arctant}\:\mathrm{dt}=\frac{\pi}{\mathrm{8}}\underset{\:\mathrm{0}} {\int}^{\:\pi} \mathrm{arctan}\left(\frac{\mathrm{1}}{\mathrm{2}}\left(\mathrm{x}−\frac{\mathrm{1}}{\mathrm{x}}\right)\mathrm{sint}\right)\mathrm{dt} \\ $$

Question Number 197374 Answers: 2 Comments: 0

Question Number 197373 Answers: 1 Comments: 0

Question Number 197371 Answers: 1 Comments: 0

Question Number 197376 Answers: 1 Comments: 0

Does anyone know how to prove this? ∫∫∫_V ((dxdydz)/(1+x^4 +y^4 +z^4 )) =((Γ^4 ((1/4)))/4^4 ) where V is the unit cube [0,1]^3 Thankyou.

$${Does}\:{anyone}\:{know}\:{how}\:{to}\:{prove}\:{this}? \\ $$$$\:\:\:\:\:\:\:\:\:\:\int\int\int_{{V}} \:\frac{{dxdydz}}{\mathrm{1}+{x}^{\mathrm{4}} +{y}^{\mathrm{4}} +{z}^{\mathrm{4}} }\:=\frac{\Gamma^{\mathrm{4}} \left(\frac{\mathrm{1}}{\mathrm{4}}\right)}{\mathrm{4}^{\mathrm{4}} } \\ $$$${where}\:{V}\:{is}\:{the}\:{unit}\:{cube}\:\left[\mathrm{0},\mathrm{1}\right]^{\mathrm{3}} \\ $$$${Thankyou}. \\ $$$$ \\ $$

Question Number 197383 Answers: 0 Comments: 1

evaluate ∫_(1/4) ^1 ∫_(√(x−x^2 )) ^(√x) ((x^2 −y^2 )/x^2 )dydx = ??

$$\:{evaluate}\:\:\int_{\mathrm{1}/\mathrm{4}} ^{\mathrm{1}} \int_{\sqrt{{x}−{x}^{\mathrm{2}} }} ^{\sqrt{{x}}} \frac{{x}^{\mathrm{2}} −{y}^{\mathrm{2}} }{{x}^{\mathrm{2}} }{dydx}\:=\:?? \\ $$

Question Number 197380 Answers: 1 Comments: 5

Question Number 197367 Answers: 1 Comments: 0

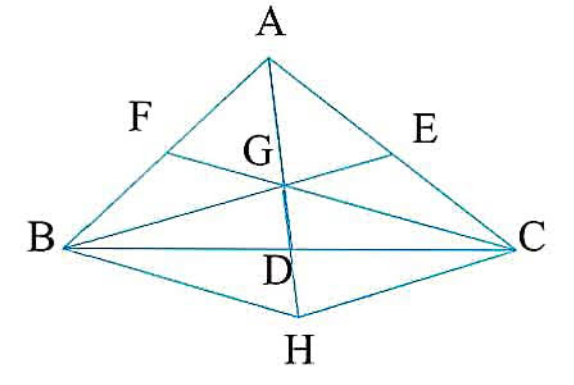
Question Number 197365 Answers: 1 Comments: 0

Question Number 197362 Answers: 2 Comments: 0

Question Number 197360 Answers: 1 Comments: 0

Find: ∫_0 ^( ∞) sin^2 ( (√x) ) e^(−x) dx = ?

$$\mathrm{Find}: \\ $$$$\int_{\mathrm{0}} ^{\:\infty} \:\mathrm{sin}^{\mathrm{2}} \:\left(\:\sqrt{\mathrm{x}}\:\right)\:\mathrm{e}^{−\boldsymbol{\mathrm{x}}} \:\mathrm{dx}\:=\:? \\ $$

Question Number 197359 Answers: 2 Comments: 1

lim_(x→0) ((1−cosxcos2x...cos(nx))/x^2 ) = ((n(n+1)(2n+1))/(12))

$$\underset{{x}\rightarrow\mathrm{0}} {\mathrm{lim}}\:\:\frac{\mathrm{1}−{cosxcos}\mathrm{2}{x}...{cos}\left({nx}\right)}{{x}^{\mathrm{2}} }\:=\:\frac{{n}\left({n}+\mathrm{1}\right)\left(\mathrm{2}{n}+\mathrm{1}\right)}{\mathrm{12}}\: \\ $$

Question Number 197349 Answers: 1 Comments: 0

calcul Σ_(n=1) ^(+oo) (−1)^(n ) ((2n+1)/(n(n+1)))

$${calcul}\: \\ $$$$\underset{{n}=\mathrm{1}} {\overset{+{oo}} {\sum}}\left(−\mathrm{1}\right)^{{n}\:} \frac{\mathrm{2}{n}+\mathrm{1}}{{n}\left({n}+\mathrm{1}\right)} \\ $$

Question Number 197346 Answers: 1 Comments: 0

Question Number 197345 Answers: 1 Comments: 0

Question Number 197344 Answers: 0 Comments: 1

((d )/dt)∙(dx^𝛌 /dt)+(1/2)g^(𝛌𝛂) (∂_𝛍 ^ g_(𝛂𝛎) +∂_𝛎 ^ g_(𝛂𝛍) −∂_𝛂 ^ g_(𝛍𝛎) )(dx^𝛍 /dt)∙(dx^𝛎 /dt)=0

$$\frac{\mathrm{d}\:\:}{\mathrm{d}{t}}\centerdot\frac{\mathrm{d}{x}^{\boldsymbol{\lambda}} }{\mathrm{d}{t}}+\frac{\mathrm{1}}{\mathrm{2}}\mathrm{g}^{\boldsymbol{\lambda\alpha}} \left(\partial_{\boldsymbol{\mu}} ^{\:} \mathrm{g}_{\boldsymbol{\alpha\nu}} +\partial_{\boldsymbol{\nu}} ^{\:} \mathrm{g}_{\boldsymbol{\alpha\mu}} −\partial_{\boldsymbol{\alpha}} ^{\:} \mathrm{g}_{\boldsymbol{\mu\nu}} \right)\frac{\mathrm{d}{x}^{\boldsymbol{\mu}} }{\mathrm{d}{t}}\centerdot\frac{\mathrm{d}{x}^{\boldsymbol{\nu}} }{\mathrm{d}{t}}=\mathrm{0} \\ $$

Question Number 197343 Answers: 0 Comments: 0

calculate ∫_0 ^(π/2) ln(cosx).ln(sinx)dx

$${calculate}\:\int_{\mathrm{0}} ^{\frac{\pi}{\mathrm{2}}} {ln}\left({cosx}\right).{ln}\left({sinx}\right){dx} \\ $$

Question Number 197338 Answers: 1 Comments: 0

∫(x^2 /(x^2 +1))dx

$$\int\frac{{x}^{\mathrm{2}} }{{x}^{\mathrm{2}} +\mathrm{1}}{dx} \\ $$

Question Number 197336 Answers: 2 Comments: 0

lim_(x→+∞) ((1/x^2 )+cosx)=?

$${lim}_{{x}\rightarrow+\infty} \left(\frac{\mathrm{1}}{{x}^{\mathrm{2}} }+\mathrm{cos}{x}\right)=? \\ $$

Question Number 197327 Answers: 2 Comments: 0

trigonometry... P = Π_(k=1) ^(44) ( 1 + tan(k) ) = ?

$$ \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:{trigonometry}... \\ $$$$ \\ $$$$\:\:\:\:\:\:\:\:\:\:\mathrm{P}\:=\:\underset{{k}=\mathrm{1}} {\overset{\mathrm{44}} {\prod}}\left(\:\:\mathrm{1}\:+\:{tan}\left({k}\right)\:\right)\:=\:?\:\: \\ $$$$ \\ $$$$\:\:\:\:\:\:\:\: \\ $$

Question Number 197335 Answers: 1 Comments: 0

Question Number 197325 Answers: 1 Comments: 0

Question Number 197323 Answers: 1 Comments: 0

If f(x)=((sin(x))/x) and S_n (α)=Σ_(k=1) ^n [f(kπ+(π/α))+f(kπ−(π/α))] (α>1) Prove that lim_(n→+∞) S_n (α)=1−f((π/α))

$$\mathrm{If}\:\mathrm{f}\left(\mathrm{x}\right)=\frac{\mathrm{sin}\left(\mathrm{x}\right)}{\mathrm{x}}\:\:\:\mathrm{and}\:\mathrm{S}_{\mathrm{n}} \left(\alpha\right)=\underset{\mathrm{k}=\mathrm{1}} {\overset{\mathrm{n}} {\sum}}\left[\mathrm{f}\left(\mathrm{k}\pi+\frac{\pi}{\alpha}\right)+\mathrm{f}\left(\mathrm{k}\pi−\frac{\pi}{\alpha}\right)\right]\:\:\:\:\left(\alpha>\mathrm{1}\right) \\ $$$$\mathrm{Prove}\:\mathrm{that}\:\underset{\mathrm{n}\rightarrow+\infty} {\:\mathrm{lim}}\:\mathrm{S}_{\mathrm{n}} \left(\alpha\right)=\mathrm{1}−\mathrm{f}\left(\frac{\pi}{\alpha}\right) \\ $$

Question Number 197320 Answers: 1 Comments: 0

Σ_(k=1) ^n (−1)^(k(k+1))

$$\underset{{k}=\mathrm{1}} {\overset{{n}} {\sum}}\left(−\mathrm{1}\right)^{{k}\left({k}+\mathrm{1}\right)} \\ $$

Question Number 197317 Answers: 0 Comments: 0

if x = ((cos θ)/u) , y = ((sin θ)/u) and z = f(x,y) then show that (∂^2 z/∂x^2 ) + (∂^2 z/∂y^2 ) = u^4 (∂^2 z/∂u^2 ) + u^3 (∂z/∂u) + u^4 (∂^2 z/∂θ^2 )

$$\:\mathrm{if}\:\:\:\mathrm{x}\:\:=\:\:\frac{\mathrm{cos}\:\theta}{\mathrm{u}}\:\:,\:\mathrm{y}\:\:=\:\frac{\mathrm{sin}\:\theta}{\mathrm{u}}\:\:{and}\:\mathrm{z}\:\:=\:\:\mathrm{f}\left(\mathrm{x},\mathrm{y}\right) \\ $$$$\mathrm{then}\:\mathrm{show}\:\mathrm{that}\: \\ $$$$\:\:\:\frac{\partial^{\mathrm{2}} \mathrm{z}}{\partial\mathrm{x}^{\mathrm{2}} }\:+\:\frac{\partial^{\mathrm{2}} \mathrm{z}}{\partial\mathrm{y}^{\mathrm{2}} }\:=\:\mathrm{u}^{\mathrm{4}} \:\frac{\partial^{\mathrm{2}} \mathrm{z}}{\partial\mathrm{u}^{\mathrm{2}} }\:+\:\mathrm{u}^{\mathrm{3}} \:\frac{\partial\mathrm{z}}{\partial\mathrm{u}}\:+\:\mathrm{u}^{\mathrm{4}} \:\frac{\partial^{\mathrm{2}} \mathrm{z}}{\partial\theta^{\mathrm{2}} } \\ $$

Question Number 197312 Answers: 1 Comments: 0

(((log_2 20)^2 −(log_2 5)^2 )/(log_2 10))=?

$$\frac{\left({log}_{\mathrm{2}} \mathrm{20}\right)^{\mathrm{2}} −\left({log}_{\mathrm{2}} \mathrm{5}\right)^{\mathrm{2}} }{{log}_{\mathrm{2}} \mathrm{10}}=? \\ $$

Pg 240 Pg 241 Pg 242 Pg 243 Pg 244 Pg 245 Pg 246 Pg 247 Pg 248 Pg 249

Contact: info@tinkutara.com