Question and Answers Forum

AllQuestion and Answers: Page 243

Question Number 195790 Answers: 1 Comments: 2

a,b,c are positive real numbers and abc =1 prove that (a−1+(1/b))(b−1+(1/c))(c−1+(1/a))≤1

$${a},{b},{c}\:{are}\:{positive}\:{real}\:{numbers}\:{and}\:{abc}\:=\mathrm{1} \\ $$$${prove}\:{that} \\ $$$$\left({a}−\mathrm{1}+\frac{\mathrm{1}}{{b}}\right)\left({b}−\mathrm{1}+\frac{\mathrm{1}}{{c}}\right)\left({c}−\mathrm{1}+\frac{\mathrm{1}}{{a}}\right)\leqslant\mathrm{1} \\ $$

Question Number 195765 Answers: 2 Comments: 0

hello { ((x^3 +(1/x^3 ) = 18)),((x>1)) :} ⇒ x^5 −(1/x^5 ) = ?

$${hello} \\ $$$$ \\ $$$$\:\begin{cases}{{x}^{\mathrm{3}} +\frac{\mathrm{1}}{{x}^{\mathrm{3}} }\:=\:\mathrm{18}}\\{{x}>\mathrm{1}}\end{cases}\:\:\Rightarrow\:\:\:{x}^{\mathrm{5}} −\frac{\mathrm{1}}{{x}^{\mathrm{5}} }\:=\:? \\ $$

Question Number 195755 Answers: 1 Comments: 0

Question Number 195753 Answers: 1 Comments: 0

Calculer ∫^( 1) _( 0) ((ln^2 t)/( (√(1−t^2 ))))dt

$$\mathrm{Calculer}\:\underset{\:\mathrm{0}} {\int}^{\:\mathrm{1}} \frac{{ln}^{\mathrm{2}} {t}}{\:\sqrt{\mathrm{1}−{t}^{\mathrm{2}} }}{dt} \\ $$

Question Number 195751 Answers: 0 Comments: 0

Question Number 195750 Answers: 1 Comments: 2

Question Number 195747 Answers: 0 Comments: 3

Question Number 195742 Answers: 1 Comments: 0

Question Number 195740 Answers: 2 Comments: 0

Question Number 195733 Answers: 1 Comments: 0

prove that Σ_(n=2) ^∞ [(B_n^_ /((n−2)!))]=((e(3−e))/((e−1)^3 )) where B_n^_ is the n− th bernouli′s number

$${prove}\:{that} \\ $$$$\underset{{n}=\mathrm{2}} {\overset{\infty} {\sum}}\left[\frac{{B}_{\overset{\_} {{n}}} }{\left({n}−\mathrm{2}\right)!}\right]=\frac{{e}\left(\mathrm{3}−{e}\right)}{\left({e}−\mathrm{1}\right)^{\mathrm{3}} } \\ $$$${where}\:{B}_{\overset{\_} {{n}}} \:{is}\:{the}\:{n}−\:{th}\:{bernouli}'{s}\:{number} \\ $$

Question Number 195732 Answers: 1 Comments: 0

((500!+499!)/(0.002))=? plz soon

$$\frac{\mathrm{500}!+\mathrm{499}!}{\mathrm{0}.\mathrm{002}}=? \\ $$$$\boldsymbol{\mathrm{plz}}\:\boldsymbol{\mathrm{soon}}\: \\ $$

Question Number 195725 Answers: 0 Comments: 1

Question Number 195722 Answers: 0 Comments: 3

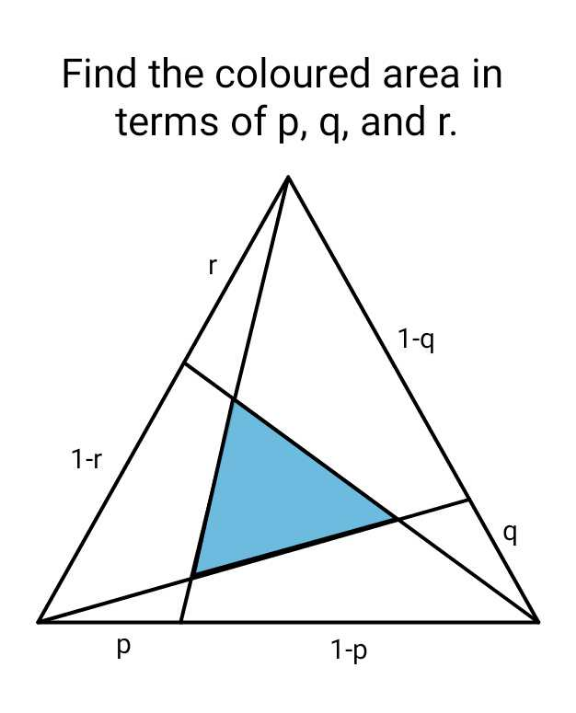
Question Number 195721 Answers: 1 Comments: 0

Question Number 195718 Answers: 1 Comments: 0

Question Number 195704 Answers: 1 Comments: 0

Question Number 195702 Answers: 1 Comments: 0

Question Number 195697 Answers: 1 Comments: 0

Question Number 195693 Answers: 2 Comments: 1

hello [Σ_(n=1) ^(10000) (1/( (√n)))]=? [ ] : is bracket thank you

$${hello} \\ $$$$\left[\underset{{n}=\mathrm{1}} {\overset{\mathrm{10000}} {\sum}}\frac{\mathrm{1}}{\:\sqrt{{n}}}\right]=? \\ $$$$\left[\:\right]\::\:{is}\:{bracket} \\ $$$${thank}\:{you} \\ $$$$ \\ $$

Question Number 195771 Answers: 2 Comments: 0

Question Number 195772 Answers: 2 Comments: 0

$$\:\:\:\:\cancel{\underline{\underbrace{ }}}\:\cancel{ } \\ $$

Question Number 195746 Answers: 1 Comments: 0

Question Number 195674 Answers: 0 Comments: 4

∫_0 ^4 ((x!)/(5!(x−5)!)) dx = ???

$$\:\:\:\int_{\mathrm{0}} ^{\mathrm{4}} \:\frac{{x}!}{\mathrm{5}!\left({x}−\mathrm{5}\right)!}\:{dx}\:=\:??? \\ $$

Question Number 195666 Answers: 1 Comments: 2

sequence of string said to be orderly if element index i different to i+1 for example aba has orderly value 2 abab has orderly value 3 abaabb has orderly value 3 if there are 7 a and 13 b example aaaaaaabbbbbbbbbbbbb has orderly value 1 what is the mean of its orderly value for all possible sequences?

$$ \\ $$$$\:{sequence}\:{of}\:{string}\:{said}\:{to}\:{be}\:{orderly} \\ $$$$\:{if}\:{element}\:{index}\:{i}\:{different}\:{to}\:{i}+\mathrm{1} \\ $$$$\:{for}\:{example} \\ $$$$\:{aba}\:{has}\:{orderly}\:{value}\:\mathrm{2} \\ $$$$\:{abab}\:{has}\:{orderly}\:{value}\:\mathrm{3} \\ $$$$\:{abaabb}\:{has}\:{orderly}\:{value}\:\mathrm{3} \\ $$$$\:{if}\:{there}\:{are}\:\mathrm{7}\:{a}\:{and}\:\mathrm{13}\:{b} \\ $$$$\:{example} \\ $$$$\:{aaaaaaabbbbbbbbbbbbb}\:{has}\:{orderly}\:{value}\:\mathrm{1} \\ $$$$\:{what}\:{is}\:{the}\:{mean}\:{of}\:{its}\:{orderly}\:{value} \\ $$$$\:{for}\:{all}\:{possible}\:{sequences}? \\ $$$$ \\ $$

Question Number 195672 Answers: 2 Comments: 0

how many different words can be formed from the letters in aaacdefgbbbb such that a “a” and a “b” are not next to each other? (see also Q#195606)

$${how}\:{many}\:{different}\:{words}\:{can}\:{be} \\ $$$${formed}\:{from}\:{the}\:{letters}\:{in} \\ $$$$\boldsymbol{{aaacdefgbbbb}} \\ $$$${such}\:{that}\:{a}\:``\boldsymbol{{a}}''\:{and}\:{a}\:``\boldsymbol{{b}}''\:{are}\:{not} \\ $$$${next}\:{to}\:{each}\:{other}? \\ $$$$ \\ $$$$\left({see}\:{also}\:{Q}#\mathrm{195606}\right) \\ $$

Question Number 195680 Answers: 0 Comments: 0

Pg 238 Pg 239 Pg 240 Pg 241 Pg 242 Pg 243 Pg 244 Pg 245 Pg 246 Pg 247

Contact: info@tinkutara.com