Question and Answers Forum

All Questions   Topic List

AllQuestion and Answers: Page 242

Question Number 196619    Answers: 1   Comments: 0

Question Number 196596    Answers: 0   Comments: 1

If f(x) = ln(((1 + x)/(1 − x))) then prove that f(((2x)/(1 + x^2 ))) = 2f(x).

$$\mathrm{If}\:{f}\left({x}\right)\:=\:\mathrm{ln}\left(\frac{\mathrm{1}\:+\:{x}}{\mathrm{1}\:−\:{x}}\right)\:\mathrm{then}\:\mathrm{prove}\:\mathrm{that} \\ $$$${f}\left(\frac{\mathrm{2}{x}}{\mathrm{1}\:+\:{x}^{\mathrm{2}} }\right)\:=\:\mathrm{2}{f}\left({x}\right). \\ $$

Question Number 196595    Answers: 0   Comments: 0

Question Number 196594    Answers: 2   Comments: 0

Question Number 196629    Answers: 1   Comments: 1

if xyz=1, prove ((x/(x−1)))^2 +((y/(y−1)))^2 +((z/(z−1)))^2 ≥1.

$${if}\:{xyz}=\mathrm{1},\:{prove} \\ $$$$\left(\frac{{x}}{{x}−\mathrm{1}}\right)^{\mathrm{2}} +\left(\frac{{y}}{{y}−\mathrm{1}}\right)^{\mathrm{2}} +\left(\frac{{z}}{{z}−\mathrm{1}}\right)^{\mathrm{2}} \geqslant\mathrm{1}. \\ $$

Question Number 196582    Answers: 1   Comments: 0

If x = log_a bc, y = log_b ca and z = log_c ab then prove that x + y + z = xyz − 2.

$$\mathrm{If}\:{x}\:=\:\mathrm{log}_{{a}} {bc},\:{y}\:=\:\mathrm{log}_{{b}} {ca}\:\mathrm{and}\:{z}\:=\:\mathrm{log}_{{c}} {ab} \\ $$$$\mathrm{then}\:\mathrm{prove}\:\mathrm{that}\:{x}\:+\:{y}\:+\:{z}\:=\:{xyz}\:−\:\mathrm{2}. \\ $$

Question Number 197585    Answers: 4   Comments: 0

f (x)=f((1/x)) ⇒ f(x)=?

$$\mathrm{f}\: \left(\mathrm{x}\right)=\mathrm{f}\left(\frac{\mathrm{1}}{\mathrm{x}}\right) \\ $$$$\Rightarrow\:\mathrm{f}\left(\mathrm{x}\right)=? \\ $$

Question Number 196576    Answers: 1   Comments: 1

Question Number 196571    Answers: 2   Comments: 0

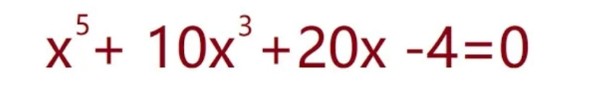
Question Number 196567    Answers: 0   Comments: 3

Show that (((1+ itanθ)/(1− itanθ)))^n =((1+ itan(nθ))/(1− tan(nθ)))

$$\mathrm{Show}\:\mathrm{that}\:\left(\frac{\mathrm{1}+\:\mathrm{itan}\theta}{\mathrm{1}−\:\mathrm{itan}\theta}\right)^{\mathrm{n}} =\frac{\mathrm{1}+\:\mathrm{itan}\left(\mathrm{n}\theta\right)}{\mathrm{1}−\:\mathrm{tan}\left(\mathrm{n}\theta\right)} \\ $$

Question Number 196565    Answers: 1   Comments: 0

find the power series exponition of f(z)=((2z+1)/(z^2 −3z+2)) about z_o = i

$${find}\:{the}\:{power}\:{series}\:{exponition}\:{of}\: \\ $$$${f}\left({z}\right)=\frac{\mathrm{2}{z}+\mathrm{1}}{{z}^{\mathrm{2}} −\mathrm{3}{z}+\mathrm{2}}\:\:{about}\:{z}_{{o}} \:=\:{i} \\ $$

Question Number 196560    Answers: 2   Comments: 1

Question Number 196559    Answers: 0   Comments: 0

Question Number 196558    Answers: 0   Comments: 0

Question Number 196557    Answers: 1   Comments: 0

Question Number 196555    Answers: 0   Comments: 0

In △ABC show that Σ ((1 + cos ∙ (A − B) ∙ cos C)/(h_C ∙ sec C)) = (3/(2 R))

$$\mathrm{In}\:\:\bigtriangleup\mathrm{ABC}\:\:\mathrm{show}\:\mathrm{that} \\ $$$$\Sigma\:\frac{\mathrm{1}\:+\:\mathrm{cos}\:\centerdot\:\left(\mathrm{A}\:−\:\mathrm{B}\right)\:\centerdot\:\mathrm{cos}\:\mathrm{C}}{\mathrm{h}_{\boldsymbol{\mathrm{C}}} \:\centerdot\:\mathrm{sec}\:\mathrm{C}}\:\:=\:\:\frac{\mathrm{3}}{\mathrm{2}\:\mathrm{R}} \\ $$

Question Number 196614    Answers: 2   Comments: 0

if S_n =(1/(1+5n))+(1/(2+5n))+(1/(3+5n))+...+(1/(6n)), find lim_(n→∞) S_n =?

$${if}\:{S}_{{n}} =\frac{\mathrm{1}}{\mathrm{1}+\mathrm{5}{n}}+\frac{\mathrm{1}}{\mathrm{2}+\mathrm{5}{n}}+\frac{\mathrm{1}}{\mathrm{3}+\mathrm{5}{n}}+...+\frac{\mathrm{1}}{\mathrm{6}{n}}, \\ $$$${find}\:\underset{{n}\rightarrow\infty} {\mathrm{lim}}{S}_{{n}} =? \\ $$

Question Number 196612    Answers: 0   Comments: 1

Question Number 196544    Answers: 1   Comments: 0

Question Number 196540    Answers: 1   Comments: 0

using definition of limit, prove lim_(x→+∞) (x/(x+1)) = 1

$$\:\:{using}\:{definition}\:{of}\:{limit},\:{prove}\: \\ $$$$\:\:\:\underset{{x}\rightarrow+\infty} {\mathrm{lim}}\frac{{x}}{{x}+\mathrm{1}}\:=\:\mathrm{1} \\ $$

Question Number 196539    Answers: 0   Comments: 0

Σ_(i=1) ^6 f(i)=Σ_(i=1) ^6 f(6+1−i) Σ_(i=1) ^6 Σ_(j=1) ^i f(i,j)=Σ_(i=1) ^6 Σ_(j=1) ^i f(6+1−j,6+1−i) Σ_(i=1) ^6 Σ_(j=1) ^i Σ_(k=1) ^j f(i,j,k)=Σ_(i=1) ^6 Σ_(j=1) ^i Σ_(k=1) ^j f(? ,? ,?)

$$\underset{{i}=\mathrm{1}} {\overset{\mathrm{6}} {\sum}}{f}\left({i}\right)=\underset{{i}=\mathrm{1}} {\overset{\mathrm{6}} {\sum}}{f}\left(\mathrm{6}+\mathrm{1}−{i}\right) \\ $$$$\underset{{i}=\mathrm{1}} {\overset{\mathrm{6}} {\sum}}\underset{{j}=\mathrm{1}} {\overset{{i}} {\sum}}{f}\left({i},{j}\right)=\underset{{i}=\mathrm{1}} {\overset{\mathrm{6}} {\sum}}\underset{{j}=\mathrm{1}} {\overset{{i}} {\sum}}{f}\left(\mathrm{6}+\mathrm{1}−{j},\mathrm{6}+\mathrm{1}−{i}\right) \\ $$$$\underset{{i}=\mathrm{1}} {\overset{\mathrm{6}} {\sum}}\underset{{j}=\mathrm{1}} {\overset{{i}} {\sum}}\underset{{k}=\mathrm{1}} {\overset{{j}} {\sum}}{f}\left({i},{j},{k}\right)=\underset{{i}=\mathrm{1}} {\overset{\mathrm{6}} {\sum}}\underset{{j}=\mathrm{1}} {\overset{{i}} {\sum}}\underset{{k}=\mathrm{1}} {\overset{{j}} {\sum}}{f}\left(?\:,?\:,?\right) \\ $$

Question Number 196534    Answers: 2   Comments: 0

lim_(x→∞) x (√(1−cos ((π/x)))) =?

$$\:\:\:\:\:\:\:\:\underset{{x}\rightarrow\infty} {\mathrm{lim}}\:\mathrm{x}\:\sqrt{\mathrm{1}−\mathrm{cos}\:\left(\frac{\pi}{\mathrm{x}}\right)}\:=? \\ $$

Question Number 196525    Answers: 1   Comments: 0

Question Number 196523    Answers: 2   Comments: 0

resoudre dans c l equation sinx=2 ★erly rolvinst★ <erly rolvinst>

$${resoudre}\:{dans}\:{c}\:{l}\:{equation}\:{sinx}=\mathrm{2}\:\:\:\:\:\bigstar{erly}\:{rolvinst}\bigstar\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:<{erly}\:{rolvinst}> \\ $$

Question Number 196522    Answers: 1   Comments: 0

Prove that ∀n∈N ∫^( n+1) _( n) lnt dt ≤ ln(∫^( n+1) _n t dt)

$$\mathrm{Prove}\:\mathrm{that}\:\forall\mathrm{n}\in\mathbb{N} \\ $$$$\underset{\:\mathrm{n}} {\int}^{\:\mathrm{n}+\mathrm{1}} \mathrm{ln}{t}\:\mathrm{dt}\:\leqslant\:\mathrm{ln}\left(\underset{\mathrm{n}} {\int}^{\:\mathrm{n}+\mathrm{1}} {t}\:\mathrm{dt}\right) \\ $$

Question Number 196519    Answers: 1   Comments: 0

if xyz=1, prove ((x/(x−1)))^2 +((y/(y−1)))^2 +((z/(z−1)))^2 ≥1.

$${if}\:{xyz}=\mathrm{1},\:{prove} \\ $$$$\left(\frac{{x}}{{x}−\mathrm{1}}\right)^{\mathrm{2}} +\left(\frac{{y}}{{y}−\mathrm{1}}\right)^{\mathrm{2}} +\left(\frac{{z}}{{z}−\mathrm{1}}\right)^{\mathrm{2}} \geqslant\mathrm{1}. \\ $$

  Pg 237      Pg 238      Pg 239      Pg 240      Pg 241      Pg 242      Pg 243      Pg 244      Pg 245      Pg 246   

Terms of Service

Privacy Policy

Contact: info@tinkutara.com