Question and Answers Forum

AllQuestion and Answers: Page 239

Question Number 196519 Answers: 1 Comments: 0

if xyz=1, prove ((x/(x−1)))^2 +((y/(y−1)))^2 +((z/(z−1)))^2 ≥1.

$${if}\:{xyz}=\mathrm{1},\:{prove} \\ $$$$\left(\frac{{x}}{{x}−\mathrm{1}}\right)^{\mathrm{2}} +\left(\frac{{y}}{{y}−\mathrm{1}}\right)^{\mathrm{2}} +\left(\frac{{z}}{{z}−\mathrm{1}}\right)^{\mathrm{2}} \geqslant\mathrm{1}. \\ $$

Question Number 196518 Answers: 1 Comments: 0

resouxre cosx=2

$${resouxre}\:{cosx}=\mathrm{2} \\ $$

Question Number 196517 Answers: 1 Comments: 0

Question Number 196516 Answers: 1 Comments: 0

Question Number 196515 Answers: 1 Comments: 0

Find: ∫_0 ^( +∞) x^𝛑 e^(−x) dx = ?

$$\mathrm{Find}:\:\:\:\int_{\mathrm{0}} ^{\:+\infty} \:\mathrm{x}^{\boldsymbol{\pi}} \:\mathrm{e}^{−\boldsymbol{\mathrm{x}}} \:\mathrm{dx}\:=\:? \\ $$

Question Number 196504 Answers: 0 Comments: 0

Question Number 196498 Answers: 1 Comments: 0

Question Number 196496 Answers: 1 Comments: 0

Question Number 196493 Answers: 1 Comments: 1

Question Number 196491 Answers: 1 Comments: 2

Question Number 196489 Answers: 0 Comments: 0

Question Number 196487 Answers: 1 Comments: 0

∫(sec^4 x−cot^4 x)dx

$$\int\left(\mathrm{sec}\:^{\mathrm{4}} {x}−\mathrm{cot}\:^{\mathrm{4}} {x}\right){dx} \\ $$

Question Number 196486 Answers: 0 Comments: 0

Question Number 196485 Answers: 1 Comments: 1

Σ_(k=o) ^n (−1)^k =?

$$\underset{{k}={o}} {\overset{{n}} {\sum}}\left(−\mathrm{1}\right)^{{k}} \:=? \\ $$

Question Number 196483 Answers: 0 Comments: 0

Question Number 196471 Answers: 1 Comments: 0

lim_(n→∞) (1/n)((1/(2 + (1/n))) + (1/(2 + (2/n))) + (1/(2 + (3/n))) + .. + (1/(2 + (n/n))))

$$\underset{\mathrm{n}\rightarrow\infty} {\mathrm{lim}}\:\frac{\mathrm{1}}{\mathrm{n}}\left(\frac{\mathrm{1}}{\mathrm{2}\:\:+\:\:\frac{\mathrm{1}}{\mathrm{n}}}\:\:+\:\:\frac{\mathrm{1}}{\mathrm{2}\:\:+\:\:\frac{\mathrm{2}}{\mathrm{n}}}\:\:+\:\:\frac{\mathrm{1}}{\mathrm{2}\:\:+\:\:\frac{\mathrm{3}}{\mathrm{n}}}\:\:+\:\:..\:\:+\:\:\frac{\mathrm{1}}{\mathrm{2}\:\:+\:\:\frac{\mathrm{n}}{\mathrm{n}}}\right) \\ $$

Question Number 196467 Answers: 1 Comments: 0

Question Number 196490 Answers: 0 Comments: 1

Know: xf(x)−f′(x)=x^2 Find f(x)=¿

$${Know}:\:{xf}\left({x}\right)−{f}'\left({x}\right)={x}^{\mathrm{2}} \\ $$$${Find}\:{f}\left({x}\right)=¿ \\ $$

Question Number 196464 Answers: 1 Comments: 0

if f(x)= x^3 +x^2 , g(x)= f^(−1) (x) , find g^′ (3) ?

$${if}\:{f}\left({x}\right)=\:{x}^{\mathrm{3}} +{x}^{\mathrm{2}} \:\:,\:{g}\left({x}\right)=\:{f}^{−\mathrm{1}} \left({x}\right)\:,\:{find}\:{g}^{'} \left(\mathrm{3}\right)\:?\:\: \\ $$

Question Number 196460 Answers: 1 Comments: 5

Question Number 196459 Answers: 1 Comments: 0

Question Number 196458 Answers: 1 Comments: 0

Question Number 196447 Answers: 2 Comments: 0

n! = 2^(25) ×3^(13) ×5^6 ×7^4 ×11^2 ×13^2 ×17×19×23 n=?

$$\:\:\:\:\mathrm{n}!\:=\:\mathrm{2}^{\mathrm{25}} ×\mathrm{3}^{\mathrm{13}} ×\mathrm{5}^{\mathrm{6}} ×\mathrm{7}^{\mathrm{4}} ×\mathrm{11}^{\mathrm{2}} ×\mathrm{13}^{\mathrm{2}} ×\mathrm{17}×\mathrm{19}×\mathrm{23} \\ $$$$\:\:\:\mathrm{n}=? \\ $$

Question Number 196444 Answers: 0 Comments: 1

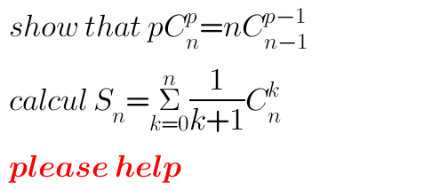
Question Number 196440 Answers: 1 Comments: 0

prove ∣v−w∣≥∣v∣−∣w∣

$${prove}\:\mid{v}−{w}\mid\geqslant\mid{v}\mid−\mid{w}\mid \\ $$

Question Number 196436 Answers: 1 Comments: 0

∫(dx/(x(x^n −1)))

$$\int\frac{{dx}}{{x}\left({x}^{{n}} −\mathrm{1}\right)} \\ $$

Pg 234 Pg 235 Pg 236 Pg 237 Pg 238 Pg 239 Pg 240 Pg 241 Pg 242 Pg 243

Contact: info@tinkutara.com