Question and Answers Forum

All Questions Topic List

AllQuestion and Answers: Page 236

Question Number 198266 Answers: 1 Comments: 0

Question Number 198263 Answers: 1 Comments: 0

Question Number 198260 Answers: 0 Comments: 0

help ! (i^→ ,j^→ ,k^→ ) est une base orthonormee. A, B, C et D sont des points de l′espace tels que : AB^(→) =i^→ +j^→ +k^→ AC^(→) =2i^→ +3j^→ +k^→ AD^(→) =i^→ −2j^→ +2k^→ . Determine tous les points P tels que (DP) ⊂ (OAB) et AP^(→) soit un vecteur unitaire orthogonal a AD^(→) . by axel

$$\mathrm{help}\:! \\ $$$$\left(\overset{\rightarrow} {{i}},\overset{\rightarrow} {{j}},\overset{\rightarrow} {{k}}\right)\:\mathrm{est}\:\mathrm{une}\:\mathrm{base}\:\mathrm{orthonormee}. \\ $$$$\mathrm{A},\:\mathrm{B},\:\mathrm{C}\:\mathrm{et}\:\mathrm{D}\:\mathrm{sont}\:\mathrm{des}\:\mathrm{points}\:\mathrm{de}\:\mathrm{l}'\mathrm{espace} \\ $$$$\mathrm{tels}\:\mathrm{que}\::\: \\ $$$$\overset{\rightarrow} {\mathrm{AB}}=\overset{\rightarrow} {{i}}+\overset{\rightarrow} {{j}}+\overset{\rightarrow} {{k}} \\ $$$$\overset{\rightarrow} {\mathrm{AC}}=\mathrm{2}\overset{\rightarrow} {{i}}+\mathrm{3}\overset{\rightarrow} {{j}}+\overset{\rightarrow} {{k}} \\ $$$$\overset{\rightarrow} {\mathrm{AD}}=\overset{\rightarrow} {{i}}−\mathrm{2}\overset{\rightarrow} {{j}}+\mathrm{2}\overset{\rightarrow} {{k}}. \\ $$$$\boldsymbol{\mathrm{Determine}}\:\boldsymbol{\mathrm{tous}}\:\boldsymbol{\mathrm{les}}\:\boldsymbol{\mathrm{points}}\:\boldsymbol{\mathrm{P}}\:\boldsymbol{\mathrm{tels}}\:\boldsymbol{\mathrm{que}}\: \\ $$$$\left(\boldsymbol{\mathrm{DP}}\right)\:\subset\:\left(\boldsymbol{\mathrm{OAB}}\right)\:\boldsymbol{\mathrm{et}}\:\overset{\rightarrow} {\boldsymbol{\mathrm{AP}}}\:\boldsymbol{\mathrm{soit}}\:\boldsymbol{\mathrm{un}}\:\boldsymbol{\mathrm{vecteur}}\: \\ $$$$\boldsymbol{\mathrm{unitaire}}\:\boldsymbol{\mathrm{orthogonal}}\:\boldsymbol{\mathrm{a}}\:\overset{\rightarrow} {\boldsymbol{\mathrm{AD}}}. \\ $$$${by}\:{axel} \\ $$

Question Number 198252 Answers: 1 Comments: 2

Question Number 198249 Answers: 1 Comments: 4

if sin(x+ϕ)+cos2x≤(√(3 )) ϕ=?

$${if}\:\:{sin}\left({x}+\varphi\right)+{cos}\mathrm{2}{x}\leqslant\sqrt{\mathrm{3}\:}\: \\ $$$$\varphi=? \\ $$

Question Number 198246 Answers: 0 Comments: 0

prove that Σ_(i=1) ^(2n−1) (((−1)^(i−1) )/i)>ln2+(1/(4n))

$${prove}\:{that} \\ $$$$\:\underset{{i}=\mathrm{1}} {\overset{\mathrm{2}{n}−\mathrm{1}} {\sum}}\frac{\left(−\mathrm{1}\right)^{{i}−\mathrm{1}} }{{i}}>{ln}\mathrm{2}+\frac{\mathrm{1}}{\mathrm{4}{n}} \\ $$

Question Number 198244 Answers: 0 Comments: 0

Question Number 198243 Answers: 3 Comments: 0

find the sum of the first n terms from 1, 2+3, 4+5+6, 7+8+9+10, ...

$${find}\:{the}\:{sum}\:{of}\:{the}\:{first}\:{n}\:{terms}\:{from} \\ $$$$\mathrm{1},\:\mathrm{2}+\mathrm{3},\:\mathrm{4}+\mathrm{5}+\mathrm{6},\:\mathrm{7}+\mathrm{8}+\mathrm{9}+\mathrm{10},\:... \\ $$

Question Number 198242 Answers: 1 Comments: 3

How many numbers with a maximum of 5 digits, greater than 4000, can be formed with the digits 2, 3, 4, 5, 6; if repetition is allowed for 2 and 3 only?

How many numbers with a maximum of 5 digits, greater than 4000, can be formed with the digits 2, 3, 4, 5, 6; if repetition is allowed for 2 and 3 only?

Question Number 198241 Answers: 1 Comments: 0

Question Number 198237 Answers: 1 Comments: 0

if −(√3)≤sin(x+ϕ)+cosx≤(√3) ϕ=?

$${if}\:\:−\sqrt{\mathrm{3}}\leqslant{sin}\left({x}+\varphi\right)+{cosx}\leqslant\sqrt{\mathrm{3}} \\ $$$$\varphi=? \\ $$

Question Number 198235 Answers: 1 Comments: 0

Question Number 198269 Answers: 1 Comments: 0

calcul Σ_(k=o) ^n sin(k)

$${calcul} \\ $$$$\underset{{k}={o}} {\overset{{n}} {\sum}}{sin}\left({k}\right) \\ $$

Question Number 198232 Answers: 1 Comments: 0

find Σ_(k=o) ^n sin(k)

$${find}\: \\ $$$$\underset{{k}={o}} {\overset{{n}} {\sum}}{sin}\left({k}\right) \\ $$

Question Number 198231 Answers: 1 Comments: 0

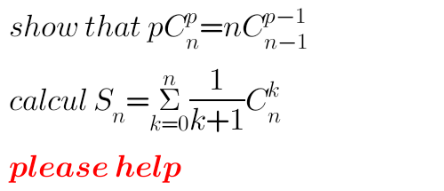
Question Number 198228 Answers: 1 Comments: 0

(4x^2 +2x+1)^(x^2 −x) >1

$$\left(\mathrm{4}{x}^{\mathrm{2}} +\mathrm{2}{x}+\mathrm{1}\right)^{{x}^{\mathrm{2}} −{x}} >\mathrm{1} \\ $$

Question Number 198222 Answers: 1 Comments: 1

log _4 (5^x −3^x ) = log _5 (4^x +3^(x ) )

$$\:\:\:\mathrm{log}\:_{\mathrm{4}} \left(\mathrm{5}^{\mathrm{x}} −\mathrm{3}^{\mathrm{x}} \right)\:=\:\mathrm{log}\:_{\mathrm{5}} \left(\mathrm{4}^{\mathrm{x}} +\mathrm{3}^{\mathrm{x}\:} \right) \\ $$

Question Number 198210 Answers: 1 Comments: 1

Red Area?

$$\:\boldsymbol{\mathrm{Red}}\:\boldsymbol{\mathrm{Area}}? \\ $$

Question Number 198207 Answers: 1 Comments: 1

((yellow Area)/(Squart Area))=?

$$\frac{\mathrm{yellow}\:\mathrm{Area}}{\mathrm{Squart}\:\mathrm{Area}}=? \\ $$

Question Number 198204 Answers: 0 Comments: 0

Question Number 198197 Answers: 1 Comments: 1

please helpe sinz = 2. Find z

$${please}\:{helpe} \\ $$$${sinz}\:=\:\mathrm{2}.\:{Find}\:{z} \\ $$

Question Number 198187 Answers: 1 Comments: 1

Question Number 198184 Answers: 1 Comments: 0

Question Number 198182 Answers: 1 Comments: 0

Question Number 198186 Answers: 1 Comments: 0

Question Number 198178 Answers: 2 Comments: 0

f(xf(y)+x)=xy+f(x) f:R→R f(x)=?

$${f}\left({xf}\left({y}\right)+{x}\right)={xy}+{f}\left({x}\right) \\ $$$${f}:\mathbb{R}\rightarrow\mathbb{R} \\ $$$${f}\left({x}\right)=? \\ $$

Pg 231 Pg 232 Pg 233 Pg 234 Pg 235 Pg 236 Pg 237 Pg 238 Pg 239 Pg 240

Terms of Service

Contact: info@tinkutara.com