Question and Answers Forum

AllQuestion and Answers: Page 235

Question Number 197524 Answers: 2 Comments: 0

Question Number 197517 Answers: 0 Comments: 0

Question Number 197514 Answers: 1 Comments: 0

lim_(x→∞) sin x sin^(−1) ((1/x))=?

$$\:\:\:\:\:\:\underset{{x}\rightarrow\infty} {\mathrm{lim}}\:\mathrm{sin}\:\mathrm{x}\:\mathrm{sin}^{−\mathrm{1}} \left(\frac{\mathrm{1}}{\mathrm{x}}\right)=? \\ $$

Question Number 197502 Answers: 0 Comments: 1

Question Number 197501 Answers: 1 Comments: 0

Question Number 197500 Answers: 1 Comments: 1

Question Number 197499 Answers: 1 Comments: 0

Question Number 197496 Answers: 2 Comments: 0

lim_(x→3) ((cos3−cosx)/(x−3))=?

$$\underset{{x}\rightarrow\mathrm{3}} {\mathrm{lim}}\frac{{cos}\mathrm{3}−{cosx}}{{x}−\mathrm{3}}=? \\ $$

Question Number 197483 Answers: 1 Comments: 0

lim_(x→−∞) ((tan^(−1) (x))/( (√(1−x)))) =?

$$\:\:\underset{{x}\rightarrow−\infty} {\mathrm{lim}}\:\frac{\mathrm{tan}^{−\mathrm{1}} \left(\mathrm{x}\right)}{\:\sqrt{\mathrm{1}−\mathrm{x}}}\:=? \\ $$

Question Number 197482 Answers: 1 Comments: 0

lim_(x→∞) sin^(−1) (((x^2 (√3) +2)/(2x^2 −3x+1)) )=?

$$\:\:\:\:\:\underset{{x}\rightarrow\infty} {\mathrm{lim}}\:\mathrm{sin}^{−\mathrm{1}} \left(\frac{\mathrm{x}^{\mathrm{2}} \sqrt{\mathrm{3}}\:+\mathrm{2}}{\mathrm{2x}^{\mathrm{2}} −\mathrm{3x}+\mathrm{1}}\:\right)=?\: \\ $$

Question Number 197479 Answers: 2 Comments: 1

find: lim_(n→∞) U_n =((n^3 +2n^2 ))^(1/3) −((n^3 −3n^2 ))^(1/3)

$$\boldsymbol{{find}}: \\ $$$$ \\ $$$$\:\:\:\:\:\:\boldsymbol{{li}}\underset{\boldsymbol{{n}}\rightarrow\infty} {\boldsymbol{{m}}}\:\boldsymbol{{U}}_{\boldsymbol{{n}}} \:=\sqrt[{\mathrm{3}}]{\boldsymbol{{n}}^{\mathrm{3}} +\mathrm{2}\boldsymbol{{n}}^{\mathrm{2}} }−\sqrt[{\mathrm{3}}]{\boldsymbol{{n}}^{\mathrm{3}} −\mathrm{3}\boldsymbol{{n}}^{\mathrm{2}} }\: \\ $$

Question Number 197476 Answers: 1 Comments: 7

find the sum (1/(x+1))+(2/(x^2 +1))+(4/(x^4 +1))+.........+(2^n /(x^2^n +1)) = ??

$$ \\ $$$$\:\:\:\mathrm{find}\:\mathrm{the}\:\mathrm{sum} \\ $$$$\:\frac{\mathrm{1}}{{x}+\mathrm{1}}+\frac{\mathrm{2}}{{x}^{\mathrm{2}} +\mathrm{1}}+\frac{\mathrm{4}}{{x}^{\mathrm{4}} +\mathrm{1}}+.........+\frac{\mathrm{2}^{{n}} }{{x}^{\mathrm{2}^{{n}} } +\mathrm{1}}\:\:=\:?? \\ $$

Question Number 197475 Answers: 3 Comments: 0

x , y ∈ R , x^( 2) + xy = 12 y^( 2) + 2xy = 7 −−−−− x , y =?

$$ \\ $$$$\:\:\:\:\:\:{x}\:,\:{y}\:\in\:\mathbb{R}\:\:\:, \\ $$$$\:\:\:\:{x}^{\:\mathrm{2}} \:+\:{xy}\:=\:\mathrm{12} \\ $$$$\:\:\:\:\:{y}^{\:\mathrm{2}} \:+\:\mathrm{2}{xy}\:=\:\mathrm{7}\: \\ $$$$\:\:\:\:−−−−−\:\:\:{x}\:,\:{y}\:=? \\ $$

Question Number 197470 Answers: 2 Comments: 0

Solve the following equation x + 2y + 2z = 0 2x + y − 2z =0 3x + 4y − 6z =0 3x − 11y + 12z = 0

$${Solve}\:{the}\:{following}\:{equation} \\ $$$${x}\:+\:\mathrm{2}{y}\:+\:\mathrm{2}{z}\:=\:\mathrm{0} \\ $$$$\mathrm{2}{x}\:+\:{y}\:−\:\mathrm{2}{z}\:=\mathrm{0} \\ $$$$\mathrm{3}{x}\:+\:\mathrm{4}{y}\:−\:\mathrm{6}{z}\:=\mathrm{0} \\ $$$$\mathrm{3}{x}\:−\:\mathrm{11}{y}\:+\:\mathrm{12}{z}\:=\:\mathrm{0} \\ $$

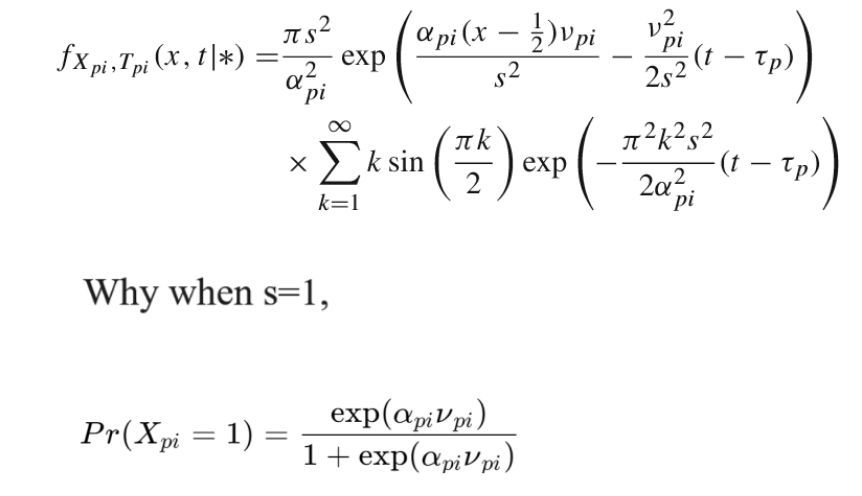
Question Number 197469 Answers: 0 Comments: 0

solve limits for functions f(x)=cos(sgn(1/x)) f(x)=sgn(cos(1/x))

$$ \\ $$$${solve}\:{limits}\:{for}\:{functions} \\ $$$${f}\left({x}\right)={cos}\left({sgn}\left(\mathrm{1}/{x}\right)\right) \\ $$$${f}\left({x}\right)={sgn}\left({cos}\left(\mathrm{1}/{x}\right)\right) \\ $$$$ \\ $$$$ \\ $$$$ \\ $$

Question Number 197464 Answers: 1 Comments: 0

Question Number 197462 Answers: 0 Comments: 1

Question Number 197459 Answers: 0 Comments: 1

Is complex infinity big? ∞^∼ =∞∙(1+i) Their absolute value is big ∣∞^∼ ∣>∣∞∣

$$\mathrm{Is}\:\mathrm{complex}\:\mathrm{infinity}\:\mathrm{big}? \\ $$$$\overset{\sim} {\infty}=\infty\centerdot\left(\mathrm{1}+{i}\right) \\ $$$$\mathrm{Their}\:\mathrm{absolute}\:\mathrm{value}\:\mathrm{is}\:\mathrm{big} \\ $$$$\mid\overset{\sim} {\infty}\mid>\mid\infty\mid \\ $$

Question Number 197455 Answers: 1 Comments: 0

f(x)=((2x+6)/2)+6−x g(x)=(√(x^(99) +x^(98) +x^(97) +.....+x)) f(g(1))+f(g(2))+.........+f(g(100))=?

$${f}\left({x}\right)=\frac{\mathrm{2}{x}+\mathrm{6}}{\mathrm{2}}+\mathrm{6}−{x} \\ $$$${g}\left({x}\right)=\sqrt{{x}^{\mathrm{99}} +{x}^{\mathrm{98}} +{x}^{\mathrm{97}} +.....+{x}} \\ $$$${f}\left({g}\left(\mathrm{1}\right)\right)+{f}\left({g}\left(\mathrm{2}\right)\right)+.........+{f}\left({g}\left(\mathrm{100}\right)\right)=? \\ $$

Question Number 197452 Answers: 1 Comments: 0

Question Number 197445 Answers: 1 Comments: 0

xe^y y′=2(e^y +x^3 e^(2x) )

$${xe}^{{y}} {y}'=\mathrm{2}\left({e}^{{y}} +{x}^{\mathrm{3}} {e}^{\mathrm{2}{x}} \right) \\ $$

Question Number 197437 Answers: 4 Comments: 0

{ ((2sin (2x+y) sin y = cos 2x)),((sin 2x−sin 2y=(√2))) :} Find the solution

$$\:\:\:\:\begin{cases}{\mathrm{2sin}\:\left(\mathrm{2}{x}+{y}\right)\:\mathrm{sin}\:{y}\:=\:\mathrm{cos}\:\mathrm{2}{x}}\\{\mathrm{sin}\:\mathrm{2}{x}−\mathrm{sin}\:\mathrm{2}{y}=\sqrt{\mathrm{2}}}\end{cases} \\ $$$$\:\:{Find}\:{the}\:{solution} \\ $$

Question Number 197436 Answers: 1 Comments: 0

∫_0 ^(π/2) (dx/(3+tan x)) =?

$$\underset{\mathrm{0}} {\overset{\pi/\mathrm{2}} {\int}}\:\frac{\mathrm{dx}}{\mathrm{3}+\mathrm{tan}\:\mathrm{x}}\:=? \\ $$

Question Number 197431 Answers: 2 Comments: 0

I = ∫_0 ^( ∞) ∫_0 ^( ∞) ∫_0 ^( ∞) ( 1+ x^2 + y^( 2) +z^( 2) )^( −(5/2)) dxdydz=?

$$ \\ $$$$ \\ $$$$\mathrm{I}\:=\:\int_{\mathrm{0}} ^{\:\infty} \int_{\mathrm{0}} ^{\:\infty} \int_{\mathrm{0}} ^{\:\infty} \left(\:\mathrm{1}+\:{x}^{\mathrm{2}} \:+\:{y}^{\:\mathrm{2}} +{z}^{\:\mathrm{2}} \right)^{\:−\frac{\mathrm{5}}{\mathrm{2}}} {dxdydz}=? \\ $$$$ \\ $$

Question Number 197422 Answers: 2 Comments: 0

Question Number 197419 Answers: 1 Comments: 0

Pg 230 Pg 231 Pg 232 Pg 233 Pg 234 Pg 235 Pg 236 Pg 237 Pg 238 Pg 239

Contact: info@tinkutara.com