
AllQuestion and Answers: Page 218
Question Number 200877 Answers: 0 Comments: 5

Question Number 200873 Answers: 1 Comments: 1

Question Number 200864 Answers: 1 Comments: 0
Question Number 200863 Answers: 1 Comments: 0

Question Number 200862 Answers: 1 Comments: 0

Question Number 200861 Answers: 1 Comments: 0

Question Number 200860 Answers: 1 Comments: 0
Question Number 200859 Answers: 0 Comments: 1
Question Number 200930 Answers: 0 Comments: 1
Question Number 200856 Answers: 0 Comments: 1

Question Number 200844 Answers: 2 Comments: 2

Question Number 200840 Answers: 2 Comments: 0
Question Number 200836 Answers: 1 Comments: 4
Question Number 200834 Answers: 1 Comments: 0
Question Number 200833 Answers: 0 Comments: 4
Question Number 200831 Answers: 0 Comments: 1

Question Number 200823 Answers: 1 Comments: 0
$${cos}\mathrm{20}\centerdot{cos}\mathrm{40}+{cos}^{\mathrm{2}} \mathrm{80}=? \\ $$
Question Number 200821 Answers: 1 Comments: 0
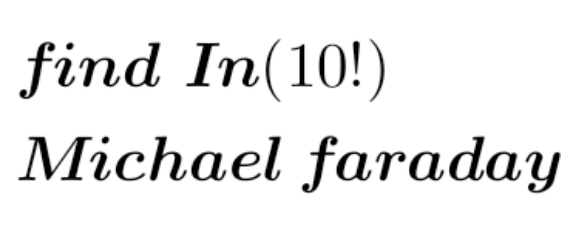
Question Number 200816 Answers: 2 Comments: 3

Question Number 200802 Answers: 1 Comments: 0

Question Number 200801 Answers: 1 Comments: 0

Question Number 200797 Answers: 0 Comments: 0

Question Number 200795 Answers: 1 Comments: 0
Question Number 200792 Answers: 1 Comments: 4

Question Number 200788 Answers: 1 Comments: 0
Question Number 200787 Answers: 0 Comments: 0

Pg 213 Pg 214 Pg 215 Pg 216 Pg 217 Pg 218 Pg 219 Pg 220 Pg 221 Pg 222
