
AllQuestion and Answers: Page 1974
Question Number 11453 Answers: 0 Comments: 0
Question Number 11444 Answers: 2 Comments: 0
Question Number 11436 Answers: 0 Comments: 1
Question Number 11433 Answers: 1 Comments: 5
Question Number 11429 Answers: 1 Comments: 0
Question Number 11425 Answers: 1 Comments: 0

Question Number 11423 Answers: 0 Comments: 0
Question Number 11420 Answers: 2 Comments: 1
Question Number 11419 Answers: 0 Comments: 1
Question Number 11417 Answers: 0 Comments: 0
Question Number 11416 Answers: 1 Comments: 0

Question Number 11413 Answers: 1 Comments: 0
Question Number 11408 Answers: 1 Comments: 0
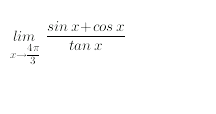
Question Number 11406 Answers: 1 Comments: 0
Question Number 11405 Answers: 1 Comments: 0
Question Number 11403 Answers: 0 Comments: 1
Question Number 11399 Answers: 1 Comments: 0
Question Number 11398 Answers: 0 Comments: 0
Question Number 11395 Answers: 0 Comments: 1
Question Number 11394 Answers: 0 Comments: 0
Question Number 11393 Answers: 0 Comments: 0

Question Number 11389 Answers: 1 Comments: 0
Question Number 11384 Answers: 1 Comments: 0
Question Number 11383 Answers: 1 Comments: 0
Question Number 11382 Answers: 0 Comments: 2
Question Number 11373 Answers: 1 Comments: 0

Pg 1969 Pg 1970 Pg 1971 Pg 1972 Pg 1973 Pg 1974 Pg 1975 Pg 1976 Pg 1977 Pg 1978
