Question and Answers Forum

AllQuestion and Answers: Page 1966

Question Number 12161 Answers: 0 Comments: 2

Question Number 12160 Answers: 1 Comments: 0

Two angles of a triangle are cot^(−1) 2 and cot^(−1) 3. Then the third angle is

$$\mathrm{Two}\:\mathrm{angles}\:\mathrm{of}\:\mathrm{a}\:\mathrm{triangle}\:\mathrm{are}\:\mathrm{cot}^{−\mathrm{1}} \mathrm{2} \\ $$$$\mathrm{and}\:\mathrm{cot}^{−\mathrm{1}} \mathrm{3}.\:\mathrm{Then}\:\mathrm{the}\:\mathrm{third}\:\mathrm{angle}\:\mathrm{is} \\ $$

Question Number 12156 Answers: 1 Comments: 0

If the ratio of the students that pass a test to those that fail is in ratio 4:1, If 9 students were chosen at random, what is the probability that exactly 7 passed the test.

$$\mathrm{If}\:\mathrm{the}\:\mathrm{ratio}\:\mathrm{of}\:\mathrm{the}\:\mathrm{students}\:\mathrm{that}\:\mathrm{pass}\:\mathrm{a}\:\mathrm{test}\:\mathrm{to}\:\mathrm{those}\:\mathrm{that}\:\mathrm{fail}\:\mathrm{is}\:\mathrm{in}\:\mathrm{ratio}\:\mathrm{4}:\mathrm{1}, \\ $$$$\mathrm{If}\:\:\mathrm{9}\:\mathrm{students}\:\mathrm{were}\:\mathrm{chosen}\:\mathrm{at}\:\mathrm{random},\:\mathrm{what}\:\mathrm{is}\:\mathrm{the}\:\mathrm{probability}\:\mathrm{that}\:\mathrm{exactly} \\ $$$$\mathrm{7}\:\mathrm{passed}\:\mathrm{the}\:\mathrm{test}. \\ $$

Question Number 12155 Answers: 1 Comments: 0

Find the 35th derivative of (2x^3 + 5x^4 )^(60)

$$\mathrm{Find}\:\mathrm{the}\:\mathrm{35th}\:\mathrm{derivative}\:\mathrm{of}\:\:\left(\mathrm{2x}^{\mathrm{3}} \:+\:\mathrm{5x}^{\mathrm{4}} \right)^{\mathrm{60}} \\ $$

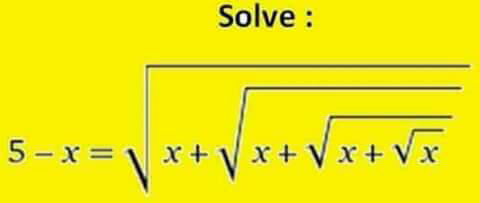
Question Number 12148 Answers: 0 Comments: 13

Question Number 12144 Answers: 1 Comments: 0

(1/(1+1^2 +1^4 ))+(2/(1+2^2 +2^4 ))+(3/(1+3^2 +3^4 ))+.....∞=?

$$\frac{\mathrm{1}}{\mathrm{1}+\mathrm{1}^{\mathrm{2}} +\mathrm{1}^{\mathrm{4}} }+\frac{\mathrm{2}}{\mathrm{1}+\mathrm{2}^{\mathrm{2}} +\mathrm{2}^{\mathrm{4}} }+\frac{\mathrm{3}}{\mathrm{1}+\mathrm{3}^{\mathrm{2}} +\mathrm{3}^{\mathrm{4}} }+.....\infty=? \\ $$

Question Number 12141 Answers: 1 Comments: 0

∫ sin(x^4 )cos(x^2 ) dx

$$\int\:\mathrm{sin}\left(\mathrm{x}^{\mathrm{4}} \right)\mathrm{cos}\left(\mathrm{x}^{\mathrm{2}} \right)\:\mathrm{dx} \\ $$

Question Number 12139 Answers: 2 Comments: 0

Find the area of the region between the graphs of f(x) = 3x^3 − x^2 − 10x and g(x) = − x^3 + 2x

$$\mathrm{Find}\:\mathrm{the}\:\mathrm{area}\:\mathrm{of}\:\mathrm{the}\:\mathrm{region}\:\mathrm{between}\:\mathrm{the}\:\mathrm{graphs}\:\mathrm{of}\:\mathrm{f}\left(\mathrm{x}\right)\:=\:\mathrm{3x}^{\mathrm{3}} \:−\:\mathrm{x}^{\mathrm{2}} \:−\:\mathrm{10x} \\ $$$$\mathrm{and}\:\mathrm{g}\left(\mathrm{x}\right)\:=\:−\:\mathrm{x}^{\mathrm{3}} \:+\:\mathrm{2x} \\ $$

Question Number 12137 Answers: 0 Comments: 0

Question Number 12130 Answers: 1 Comments: 0

∫(√(a+x/a−x )) −(√(a−x/a+x))

$$\int\sqrt{{a}+{x}/{a}−{x}\:} \\ $$$$−\sqrt{{a}−{x}/{a}+{x}} \\ $$

Question Number 12127 Answers: 1 Comments: 1

Question Number 12126 Answers: 1 Comments: 0

Question Number 12132 Answers: 1 Comments: 0

Given that 1° = 0.017 rad Use f(a) = sin(a) to find an approximate value for sin(29)°.

$$\mathrm{Given}\:\mathrm{that}\:\:\mathrm{1}°\:=\:\mathrm{0}.\mathrm{017}\:\mathrm{rad} \\ $$$$\mathrm{Use}\:\:\mathrm{f}\left(\mathrm{a}\right)\:=\:\mathrm{sin}\left(\mathrm{a}\right)\:\mathrm{to}\:\mathrm{find}\:\mathrm{an}\:\mathrm{approximate}\:\mathrm{value}\:\mathrm{for}\:\mathrm{sin}\left(\mathrm{29}\right)°. \\ $$

Question Number 12131 Answers: 0 Comments: 0

a cube has a rib ABCD.EFGH, the midle point P on BF so that BP = PF, and the midle point Q on FG so that FQ = QG how long projection point C to APQH field ?

$${a}\:{cube}\:{has}\:{a}\:{rib}\:{ABCD}.{EFGH},\:{the}\:{midle}\:{point}\:{P}\:\:{on}\:{BF}\:{so}\:{that}\:{BP}\:=\:{PF}, \\ $$$${and}\:{the}\:{midle}\:{point}\:{Q}\:{on}\:{FG}\:{so}\:{that}\:{FQ}\:=\:{QG} \\ $$$${how}\:{long}\:{projection}\:{point}\:{C}\:{to}\:{APQH}\:{field}\:? \\ $$

Question Number 12111 Answers: 0 Comments: 0

show that: Σ_(n=0) ^∞ (((−1)^n )/(n!))=(1/e) please show your working

$$\mathrm{show}\:\mathrm{that}: \\ $$$$\underset{{n}=\mathrm{0}} {\overset{\infty} {\sum}}\frac{\left(−\mathrm{1}\right)^{{n}} }{{n}!}=\frac{\mathrm{1}}{{e}} \\ $$$$\mathrm{please}\:\mathrm{show}\:\mathrm{your}\:\mathrm{working} \\ $$

Question Number 12109 Answers: 0 Comments: 0

show that: Σ_(n=1) ^∞ (((−1)^(n+1) )/n)=ln(2) please show your working

$$\mathrm{show}\:\mathrm{that}: \\ $$$$\underset{{n}=\mathrm{1}} {\overset{\infty} {\sum}}\frac{\left(−\mathrm{1}\right)^{{n}+\mathrm{1}} }{{n}}=\mathrm{ln}\left(\mathrm{2}\right) \\ $$$$\mathrm{please}\:\mathrm{show}\:\mathrm{your}\:\mathrm{working} \\ $$

Question Number 12107 Answers: 1 Comments: 2

10^3 + 11^3 + 12^3 + ... + 20^3 Is there any ways to count the sum of that sequence without sum them manually?

$$\mathrm{10}^{\mathrm{3}} \:+\:\mathrm{11}^{\mathrm{3}} \:+\:\mathrm{12}^{\mathrm{3}} \:+\:...\:+\:\mathrm{20}^{\mathrm{3}} \\ $$$$\mathrm{Is}\:\mathrm{there}\:\mathrm{any}\:\mathrm{ways}\:\mathrm{to}\:\mathrm{count}\:\mathrm{the}\:\mathrm{sum}\: \\ $$$$\mathrm{of}\:\mathrm{that}\:\mathrm{sequence}\:\mathrm{without}\:\mathrm{sum}\:\mathrm{them}\:\mathrm{manually}? \\ $$

Question Number 12106 Answers: 1 Comments: 0