Question and Answers Forum

AllQuestion and Answers: Page 1961

Question Number 12405 Answers: 0 Comments: 1

how to prove that there exist infinitely many rationals between any two irrationals?

$${how}\:{to}\:{prove}\:{that}\:{there}\:{exist}\:{infinitely}\:{many}\:{rationals}\:{between}\:{any}\:{two}\:{irrationals}? \\ $$$$ \\ $$

Question Number 12403 Answers: 1 Comments: 0

f(x)=⌊x−(3/e)⌋+⌊x+(3/e)⌋⇒f(1)=?

$${f}\left({x}\right)=\lfloor{x}−\frac{\mathrm{3}}{{e}}\rfloor+\lfloor{x}+\frac{\mathrm{3}}{{e}}\rfloor\Rightarrow{f}\left(\mathrm{1}\right)=? \\ $$

Question Number 12402 Answers: 0 Comments: 2

12sgn(x^2 −x−20)+3≥0⇒ (ss)=?

$$\mathrm{12}{sgn}\left({x}^{\mathrm{2}} −{x}−\mathrm{20}\right)+\mathrm{3}\geqslant\mathrm{0}\Rightarrow \\ $$$$\left({ss}\right)=? \\ $$

Question Number 12401 Answers: 1 Comments: 1

∫_0 ^(2π) sgn(cosx)dx=?

$$\int_{\mathrm{0}} ^{\mathrm{2}\pi} {sgn}\left({cosx}\right){dx}=? \\ $$

Question Number 12394 Answers: 0 Comments: 0

Question Number 12386 Answers: 2 Comments: 0

f(x + (1/x)) = ((x^6 + 1)/(27)) f(x) = ?

$${f}\left({x}\:+\:\frac{\mathrm{1}}{{x}}\right)\:=\:\frac{{x}^{\mathrm{6}} \:+\:\mathrm{1}}{\mathrm{27}} \\ $$$${f}\left({x}\right)\:=\:? \\ $$

Question Number 12382 Answers: 2 Comments: 0

lim_(x→0) ((ln cos(3x))/(ln cos(2x)))

$$\underset{{x}\rightarrow\mathrm{0}} {\mathrm{lim}}\:\:\:\frac{\mathrm{ln}\:\mathrm{cos}\left(\mathrm{3x}\right)}{\mathrm{ln}\:\mathrm{cos}\left(\mathrm{2x}\right)} \\ $$

Question Number 12377 Answers: 3 Comments: 0

∫ ((√(1 + (√x)))/x) dx

$$\int\:\:\frac{\sqrt{\mathrm{1}\:+\:\sqrt{\mathrm{x}}}}{\mathrm{x}}\:\:\mathrm{dx} \\ $$

Question Number 12378 Answers: 1 Comments: 2

Prove that, sinθ + 2cosθ = 1

$$\mathrm{Prove}\:\mathrm{that}, \\ $$$$\mathrm{sin}\theta\:+\:\mathrm{2cos}\theta\:=\:\mathrm{1} \\ $$

Question Number 12368 Answers: 1 Comments: 0

Question Number 12365 Answers: 0 Comments: 5

Question Number 12361 Answers: 1 Comments: 0

((√2) +(√3) +2 + (√5))(−(√2) + (√3) + 2 − (√5))((√(10)) + 2(√3)) Can you solve this without solving them manually?

$$\left(\sqrt{\mathrm{2}}\:+\sqrt{\mathrm{3}}\:+\mathrm{2}\:+\:\sqrt{\mathrm{5}}\right)\left(−\sqrt{\mathrm{2}}\:+\:\sqrt{\mathrm{3}}\:+\:\mathrm{2}\:−\:\sqrt{\mathrm{5}}\right)\left(\sqrt{\mathrm{10}}\:+\:\mathrm{2}\sqrt{\mathrm{3}}\right) \\ $$$$ \\ $$$$\mathrm{Can}\:\mathrm{you}\:\mathrm{solve}\:\mathrm{this}\:\mathrm{without}\:\mathrm{solving}\:\mathrm{them}\:\mathrm{manually}? \\ $$

Question Number 12359 Answers: 1 Comments: 0

Question Number 12371 Answers: 0 Comments: 0

tank you

$${tank}\:{you} \\ $$$$ \\ $$

Question Number 12332 Answers: 2 Comments: 7

prove ; ((0/0))=2

$$\mathrm{prove}\:;\:\left(\frac{\mathrm{0}}{\mathrm{0}}\right)=\mathrm{2} \\ $$

Question Number 12331 Answers: 2 Comments: 0

Question Number 12330 Answers: 0 Comments: 0

find the fifth digit from the end of the number 5^5^5^4^5

$$\mathrm{find}\:\mathrm{the}\:\mathrm{fifth}\:\mathrm{digit}\:\mathrm{from}\:\mathrm{the}\:\mathrm{end} \\ $$$$\mathrm{of}\:\mathrm{the}\:\mathrm{number} \\ $$$$\mathrm{5}^{\mathrm{5}^{\mathrm{5}^{\mathrm{4}^{\mathrm{5}} } } } \\ $$

Question Number 12329 Answers: 2 Comments: 2

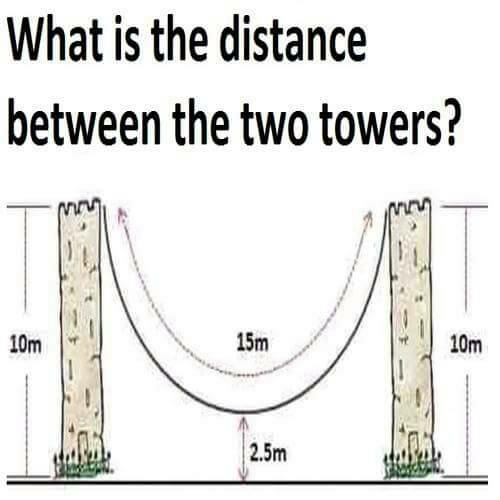
Question Number 12328 Answers: 1 Comments: 0

if it′s correct solve plz lim_(x→0) ((x^x −1)/(xlnx))

$$\boldsymbol{\mathrm{if}}\:\boldsymbol{\mathrm{it}}'\boldsymbol{\mathrm{s}}\:\boldsymbol{\mathrm{correct}}\:\boldsymbol{\mathrm{solve}}\:\boldsymbol{\mathrm{plz}} \\ $$$$\underset{\boldsymbol{\mathrm{x}}\rightarrow\mathrm{0}} {\boldsymbol{\mathrm{lim}}}\frac{\boldsymbol{\mathrm{x}}^{\boldsymbol{\mathrm{x}}} −\mathrm{1}}{\boldsymbol{\mathrm{xlnx}}} \\ $$

Question Number 12321 Answers: 0 Comments: 0

When a known standard resistor of 2.0 Ω is connected to the 0.0 cm end of a meter bridge. The balance point is found to be at 55.0cm. What is the value of the resistor.

$$\mathrm{When}\:\mathrm{a}\:\mathrm{known}\:\mathrm{standard}\:\mathrm{resistor}\:\mathrm{of}\:\mathrm{2}.\mathrm{0}\:\Omega\:\mathrm{is}\:\mathrm{connected}\:\mathrm{to}\:\mathrm{the}\:\mathrm{0}.\mathrm{0}\:\mathrm{cm}\:\mathrm{end}\:\mathrm{of} \\ $$$$\mathrm{a}\:\mathrm{meter}\:\mathrm{bridge}.\:\mathrm{The}\:\mathrm{balance}\:\mathrm{point}\:\mathrm{is}\:\mathrm{found}\:\mathrm{to}\:\mathrm{be}\:\mathrm{at}\:\mathrm{55}.\mathrm{0cm}.\:\mathrm{What}\:\mathrm{is}\:\mathrm{the}\: \\ $$$$\mathrm{value}\:\mathrm{of}\:\mathrm{the}\:\mathrm{resistor}. \\ $$

Question Number 12319 Answers: 1 Comments: 0

Question Number 12316 Answers: 1 Comments: 0

What is the acceleration due to gravity , g, on the moon , if g is 10m/s^2 on the earth.

$$\mathrm{What}\:\mathrm{is}\:\mathrm{the}\:\mathrm{acceleration}\:\mathrm{due}\:\mathrm{to}\:\mathrm{gravity}\:,\:\mathrm{g},\:\mathrm{on}\:\mathrm{the}\:\mathrm{moon}\:,\:\mathrm{if}\:\mathrm{g}\:\mathrm{is}\:\mathrm{10m}/\mathrm{s}^{\mathrm{2}} \:\mathrm{on} \\ $$$$\mathrm{the}\:\mathrm{earth}. \\ $$

Question Number 12306 Answers: 1 Comments: 0

Two similar boxes B_i (i=1,2)contain (i+1)red and (5−i−1) black balls. One box is chosen at random and two balls are drawn randomly. what is the probability that both balls are of different colours? (a) 1/2 (b) 3/10 (c) 2/5 (d) 3/5

Question Number 12305 Answers: 1 Comments: 0

If c>0 and 4a+c<2b,then ax^2 −bx+c=0 has a root in which intervals? (a) (0,2) (b) (2,3) (c) (3,4) (d) (−2,0)

$${If}\:{c}>\mathrm{0}\:{and}\:\mathrm{4}{a}+{c}<\mathrm{2}{b},{then} \\ $$$${ax}^{\mathrm{2}} −{bx}+{c}=\mathrm{0}\:{has}\:{a}\:{root}\:{in}\:{which} \\ $$$${intervals}? \\ $$$$\left({a}\right)\:\:\left(\mathrm{0},\mathrm{2}\right) \\ $$$$\left({b}\right)\:\:\left(\mathrm{2},\mathrm{3}\right) \\ $$$$\left({c}\right)\:\:\left(\mathrm{3},\mathrm{4}\right) \\ $$$$\left({d}\right)\:\:\left(−\mathrm{2},\mathrm{0}\right) \\ $$

Question Number 12304 Answers: 1 Comments: 0

How many geometric progressions is/are possible contauning 27,8 and 12 as three of its/their terms? (a) 1 (b) 2 (c) 4 (d) infinitely many

$${How}\:{many}\:{geometric}\:{progressions} \\ $$$${is}/{are}\:{possible}\:{contauning}\:\mathrm{27},\mathrm{8} \\ $$$${and}\:\mathrm{12}\:{as}\:{three}\:{of}\:{its}/{their}\:{terms}? \\ $$$$\left({a}\right)\:\:\mathrm{1} \\ $$$$\left({b}\right)\:\:\mathrm{2} \\ $$$$\left({c}\right)\:\:\mathrm{4} \\ $$$$\left({d}\right)\:\:{infinitely}\:{many} \\ $$$$ \\ $$

Question Number 12303 Answers: 1 Comments: 0

What is∫_1 ^3 ∣1−x^4 ∣dx equal to? (a) −232/5 (b) −116/5 (c) 116/5 (d) 232/5

$${What}\:{is}\underset{\mathrm{1}} {\overset{\mathrm{3}} {\int}}\mid\mathrm{1}−{x}^{\mathrm{4}} \:\mid{dx}\:{equal}\:{to}? \\ $$$$\left({a}\right)\:\:−\mathrm{232}/\mathrm{5} \\ $$$$\left({b}\right)\:\:−\mathrm{116}/\mathrm{5} \\ $$$$\left({c}\right)\:\:\:\mathrm{116}/\mathrm{5} \\ $$$$\left({d}\right)\:\:\:\mathrm{232}/\mathrm{5} \\ $$

Pg 1956 Pg 1957 Pg 1958 Pg 1959 Pg 1960 Pg 1961 Pg 1962 Pg 1963 Pg 1964 Pg 1965

Contact: info@tinkutara.com