Question and Answers Forum

AllQuestion and Answers: Page 1958

Question Number 11383 Answers: 1 Comments: 0

There are six trains travelling between Abuja and Lagos and back. In how many ways can a man travel from abuja to Lagos by one train and return by a different train

$$\mathrm{There}\:\mathrm{are}\:\mathrm{six}\:\mathrm{trains}\:\mathrm{travelling}\:\mathrm{between}\:\mathrm{Abuja}\:\mathrm{and}\:\mathrm{Lagos}\:\mathrm{and}\:\mathrm{back}. \\ $$$$\mathrm{In}\:\mathrm{how}\:\mathrm{many}\:\mathrm{ways}\:\mathrm{can}\:\mathrm{a}\:\mathrm{man}\:\mathrm{travel}\:\mathrm{from}\:\mathrm{abuja}\:\mathrm{to}\:\mathrm{Lagos}\:\mathrm{by}\:\mathrm{one}\:\mathrm{train}\:\mathrm{and} \\ $$$$\mathrm{return}\:\mathrm{by}\:\mathrm{a}\:\mathrm{different}\:\mathrm{train} \\ $$

Question Number 11382 Answers: 0 Comments: 2

In how many ways can 24 different articles be divided into groups of 12, 8 and 4 articles respectively

$$\mathrm{In}\:\mathrm{how}\:\mathrm{many}\:\mathrm{ways}\:\mathrm{can}\:\mathrm{24}\:\mathrm{different}\:\mathrm{articles}\:\mathrm{be}\:\mathrm{divided}\:\mathrm{into}\:\mathrm{groups}\:\mathrm{of} \\ $$$$\mathrm{12},\:\mathrm{8}\:\mathrm{and}\:\mathrm{4}\:\mathrm{articles}\:\mathrm{respectively} \\ $$

Question Number 11373 Answers: 1 Comments: 0

Question Number 11372 Answers: 0 Comments: 0

If G_1 and G_2 are groups , and f : G_1 →G_2 is a group homomorphism , then prove that o(G_1 ) = o(G_2 ) .

$$\mathrm{If}\:\mathrm{G}_{\mathrm{1}} \:\mathrm{and}\:\mathrm{G}_{\mathrm{2}} \:\mathrm{are}\:\mathrm{groups}\:,\:\mathrm{and}\:\mathrm{f}\::\:\mathrm{G}_{\mathrm{1}} \:\rightarrow\mathrm{G}_{\mathrm{2}} \\ $$$$\mathrm{is}\:\mathrm{a}\:\mathrm{group}\:\mathrm{homomorphism}\:,\:\mathrm{then}\:\mathrm{prove} \\ $$$$\mathrm{that}\:\mathrm{o}\left(\mathrm{G}_{\mathrm{1}} \right)\:=\:\mathrm{o}\left(\mathrm{G}_{\mathrm{2}} \right)\:. \\ $$

Question Number 11365 Answers: 0 Comments: 1

∅(n)=n−1 , n∈Z ,where ∅ is Eular phi function. True or false .And explain it .

$$\emptyset\left(\mathrm{n}\right)=\mathrm{n}−\mathrm{1}\:,\:\mathrm{n}\in\mathrm{Z}\:,\mathrm{where}\:\emptyset\:\mathrm{is}\:\mathrm{Eular}\:\mathrm{phi}\:\mathrm{function}. \\ $$$$\mathrm{True}\:\mathrm{or}\:\mathrm{false}\:.\mathrm{And}\:\mathrm{explain}\:\mathrm{it}\:. \\ $$

Question Number 11364 Answers: 1 Comments: 0

lim_(x→0) (((√(1 + tan x)) − (√(1 + sin x)))/x^3 )

$$\underset{{x}\rightarrow\mathrm{0}} {\mathrm{lim}}\:\:\frac{\sqrt{\mathrm{1}\:+\:\mathrm{tan}\:{x}}\:−\:\sqrt{\mathrm{1}\:+\:\mathrm{sin}\:{x}}}{{x}^{\mathrm{3}} } \\ $$

Question Number 11363 Answers: 0 Comments: 0

x∈Z f(x)=log_3 (((x−5)/(x−2)))⇒Σx=?

$$\mathrm{x}\in\mathrm{Z} \\ $$$$\mathrm{f}\left(\mathrm{x}\right)=\mathrm{log}_{\mathrm{3}} \left(\frac{\mathrm{x}−\mathrm{5}}{\mathrm{x}−\mathrm{2}}\right)\Rightarrow\Sigma\mathrm{x}=? \\ $$

Question Number 11356 Answers: 1 Comments: 0

Question Number 11355 Answers: 1 Comments: 0

z+3−2i=(1+i)×z^− ⇒∣z∣=?

$$\mathrm{z}+\mathrm{3}−\mathrm{2i}=\left(\mathrm{1}+\mathrm{i}\right)×\overset{−} {\mathrm{z}}\:\Rightarrow\mid\mathrm{z}\mid=? \\ $$

Question Number 11353 Answers: 0 Comments: 0

reduce the matrix below to echelon form and then to row canonical form A = [((2 4 2 −2 5 1)),((3 6 2 2 0 4)),((4 8 2 6 −5 7)) ]

$$\mathrm{reduce}\:\mathrm{the}\:\mathrm{matrix}\:\mathrm{below}\:\mathrm{to}\:\mathrm{echelon}\:\mathrm{form}\:\mathrm{and}\:\mathrm{then}\:\mathrm{to}\:\mathrm{row}\:\mathrm{canonical}\:\mathrm{form} \\ $$$$\mathrm{A}\:=\:\begin{bmatrix}{\mathrm{2}\:\:\mathrm{4}\:\:\mathrm{2}\:\:−\mathrm{2}\:\:\mathrm{5}\:\:\mathrm{1}}\\{\mathrm{3}\:\:\mathrm{6}\:\:\mathrm{2}\:\:\:\:\:\mathrm{2}\:\:\mathrm{0}\:\:\mathrm{4}}\\{\mathrm{4}\:\:\mathrm{8}\:\:\mathrm{2}\:\:\:\mathrm{6}\:\:−\mathrm{5}\:\mathrm{7}}\end{bmatrix} \\ $$

Question Number 11352 Answers: 1 Comments: 0

if, A = x^2 sin yi + z^2 cos yj − xy^2 k, find, dA

$$\mathrm{if},\:\:\mathrm{A}\:=\:\mathrm{x}^{\mathrm{2}} \:\mathrm{sin}\:\mathrm{yi}\:+\:\mathrm{z}^{\mathrm{2}} \:\mathrm{cos}\:\mathrm{yj}\:−\:\mathrm{xy}^{\mathrm{2}} \mathrm{k},\:\:\mathrm{find},\:\:\mathrm{dA}\:\: \\ $$

Question Number 11388 Answers: 0 Comments: 0

A cell supplies a current of 6 ameter through a 2 coil and a current of 0.2 ameter through 7 coil. Calculate the limits and the internal resistance of the cell

$$\mathrm{A}\:\mathrm{cell}\:\mathrm{supplies}\:\mathrm{a}\:\mathrm{current}\:\mathrm{of}\:\mathrm{6}\:\mathrm{ameter}\:\mathrm{through}\:\mathrm{a}\:\mathrm{2}\:\mathrm{coil}\:\mathrm{and}\:\mathrm{a}\:\mathrm{current}\:\mathrm{of}\:\mathrm{0}.\mathrm{2}\: \\ $$$$\mathrm{ameter}\:\mathrm{through}\:\mathrm{7}\:\mathrm{coil}.\:\mathrm{Calculate}\:\mathrm{the}\:\mathrm{limits}\:\mathrm{and}\:\mathrm{the}\:\mathrm{internal}\:\mathrm{resistance} \\ $$$$\mathrm{of}\:\mathrm{the}\:\mathrm{cell} \\ $$

Question Number 11351 Answers: 0 Comments: 0

Find the workdone in moving a paticle once around an ellipse C in the xy plane. if the ellipse has centre at the origin with semi major and semi minor axes 4 and 3 respectively.

$$\mathrm{Find}\:\mathrm{the}\:\mathrm{workdone}\:\mathrm{in}\:\mathrm{moving}\:\mathrm{a}\:\mathrm{paticle}\:\mathrm{once}\:\mathrm{around}\:\mathrm{an}\:\mathrm{ellipse}\:\mathrm{C}\:\mathrm{in}\:\mathrm{the} \\ $$$$\mathrm{xy}\:\mathrm{plane}.\:\mathrm{if}\:\mathrm{the}\:\mathrm{ellipse}\:\mathrm{has}\:\mathrm{centre}\:\mathrm{at}\:\mathrm{the}\:\mathrm{origin}\:\mathrm{with}\:\mathrm{semi}\:\mathrm{major}\:\mathrm{and}\:\mathrm{semi}\:\mathrm{minor}\:\mathrm{axes}\: \\ $$$$\mathrm{4}\:\mathrm{and}\:\mathrm{3}\:\mathrm{respectively}. \\ $$

Question Number 11344 Answers: 0 Comments: 1

n_c_n =((n!)/((n−n)!n!))

$${n}_{{c}_{{n}} } =\frac{{n}!}{\left({n}−{n}\right)!{n}!} \\ $$

Question Number 11343 Answers: 0 Comments: 1

n_c_n =((n1)/((n−n)))

$${n}_{\boldsymbol{\mathrm{c}}_{\boldsymbol{\mathrm{n}}} } =\frac{{n}\mathrm{1}}{\left({n}−{n}\right)} \\ $$

Question Number 11341 Answers: 0 Comments: 2

Question Number 11338 Answers: 2 Comments: 1

Question Number 11334 Answers: 1 Comments: 0

z+∣z∣=9−3i⇒Re(z)

$$\mathrm{z}+\mid\mathrm{z}\mid=\mathrm{9}−\mathrm{3i}\Rightarrow\mathrm{Re}\left(\mathrm{z}\right) \\ $$

Question Number 11332 Answers: 0 Comments: 0

Question Number 11327 Answers: 0 Comments: 0

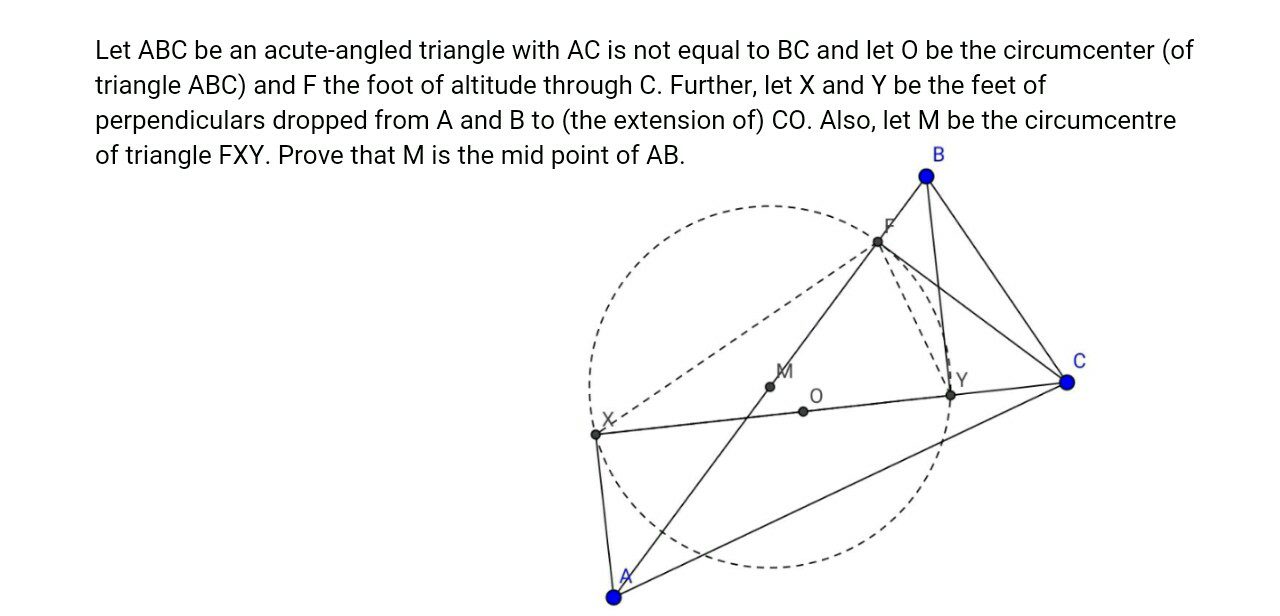
pl show me typing and shape drawing app for mobile.

$$\mathrm{pl}\:\mathrm{show}\:\mathrm{me}\:\mathrm{typing}\:\mathrm{and}\:\mathrm{shape}\:\mathrm{drawing}\:\mathrm{app}\:\mathrm{for}\:\mathrm{mobile}. \\ $$

Question Number 11321 Answers: 2 Comments: 2

How many solution {x, y, z} that fulfilled x + y + z = 99 ? x,y,z ∈ N

$$\mathrm{How}\:\mathrm{many}\:\mathrm{solution}\:\left\{{x},\:{y},\:{z}\right\}\:\mathrm{that}\:\mathrm{fulfilled} \\ $$$${x}\:+\:{y}\:+\:{z}\:=\:\mathrm{99}\:? \\ $$$${x},{y},{z}\:\in\:\mathbb{N} \\ $$

Question Number 11309 Answers: 0 Comments: 4

ax^2 +by^2 +cz^2 =r^2 Point P=(a, b, c) Point Q=(l, m, n) Both points lie on the curve what is the shortest path from point P to Q, along the outside of the curve?

$${ax}^{\mathrm{2}} +{by}^{\mathrm{2}} +{cz}^{\mathrm{2}} ={r}^{\mathrm{2}} \\ $$$$\: \\ $$$$\mathrm{Point}\:{P}=\left({a},\:{b},\:{c}\right) \\ $$$$\mathrm{Point}\:{Q}=\left({l},\:{m},\:{n}\right) \\ $$$$\mathrm{Both}\:\mathrm{points}\:\mathrm{lie}\:\mathrm{on}\:\mathrm{the}\:\mathrm{curve} \\ $$$$\: \\ $$$$\mathrm{what}\:\mathrm{is}\:\mathrm{the}\:\mathrm{shortest}\:\mathrm{path}\:\mathrm{from}\:\mathrm{point} \\ $$$${P}\:\mathrm{to}\:{Q},\:\mathrm{along}\:\mathrm{the}\:\mathrm{outside}\:\mathrm{of}\:\mathrm{the}\:\mathrm{curve}? \\ $$

Question Number 11315 Answers: 0 Comments: 6

Question Number 11303 Answers: 2 Comments: 0

Find the equation and radius of the circumference of the triangle formed by the three lines. 2y − 9x + 26 = 0 9y + 2x + 32 = 0 11y − 7x − 27 = 0

$$\mathrm{Find}\:\mathrm{the}\:\mathrm{equation}\:\mathrm{and}\:\mathrm{radius}\:\mathrm{of}\:\mathrm{the}\:\mathrm{circumference}\:\mathrm{of}\:\mathrm{the}\:\mathrm{triangle}\:\mathrm{formed} \\ $$$$\mathrm{by}\:\mathrm{the}\:\mathrm{three}\:\mathrm{lines}. \\ $$$$\mathrm{2y}\:−\:\mathrm{9x}\:+\:\mathrm{26}\:=\:\mathrm{0} \\ $$$$\mathrm{9y}\:+\:\mathrm{2x}\:+\:\mathrm{32}\:=\:\mathrm{0} \\ $$$$\mathrm{11y}\:−\:\mathrm{7x}\:−\:\mathrm{27}\:=\:\mathrm{0} \\ $$

Question Number 11302 Answers: 2 Comments: 0

((sin10x−sin6x−sin2x)/(sin9x−sin7x−sinx))=?

$$\frac{\mathrm{sin10x}−\mathrm{sin6x}−\mathrm{sin2x}}{\mathrm{sin9x}−\mathrm{sin7x}−\mathrm{sinx}}=? \\ $$

Question Number 11299 Answers: 0 Comments: 0

Define two partition p_1 and p_2 of [2,5] such that p_1 ⊂p_2 . Find the upper and lower product sums with respet to f ,?defined by f(x)=x , x<4 =1−x^2 , x ≥4 . Also verify the relationship between these 4 sums.

$$\mathrm{Define}\:\mathrm{two}\:\mathrm{partition}\:\mathrm{p}_{\mathrm{1}} \:\mathrm{and}\:\mathrm{p}_{\mathrm{2}} \:\mathrm{of}\:\left[\mathrm{2},\mathrm{5}\right]\:\mathrm{such}\:\mathrm{that} \\ $$$$\mathrm{p}_{\mathrm{1}} \subset\mathrm{p}_{\mathrm{2}} \:.\:\mathrm{Find}\:\mathrm{the}\:\mathrm{upper}\:\mathrm{and}\:\mathrm{lower}\:\mathrm{product} \\ $$$$\mathrm{sums}\:\mathrm{with}\:\mathrm{respet}\:\mathrm{to}\:\mathrm{f}\:,?\mathrm{defined}\:\mathrm{by} \\ $$$$\mathrm{f}\left(\mathrm{x}\right)=\mathrm{x}\:,\:\:\:\:\:\:\:\:\:\:\:\:\:\mathrm{x}<\mathrm{4} \\ $$$$\:\:\:\:\:\:\:\:=\mathrm{1}−\mathrm{x}^{\mathrm{2}} \:,\:\:\:\:\:\mathrm{x}\:\geqslant\mathrm{4}\:\:. \\ $$$$\mathrm{Also}\:\mathrm{verify}\:\mathrm{the}\:\mathrm{relationship}\:\mathrm{between}\:\mathrm{these} \\ $$$$\mathrm{4}\:\mathrm{sums}. \\ $$

Pg 1953 Pg 1954 Pg 1955 Pg 1956 Pg 1957 Pg 1958 Pg 1959 Pg 1960 Pg 1961 Pg 1962

Contact: info@tinkutara.com