
AllQuestion and Answers: Page 1957
Question Number 13260 Answers: 2 Comments: 0
Question Number 13295 Answers: 1 Comments: 3
Question Number 13257 Answers: 1 Comments: 0

Question Number 13258 Answers: 1 Comments: 0

Question Number 13252 Answers: 1 Comments: 0
$$\underset{{x}\rightarrow\mathrm{0}} {\mathrm{lim}sin}\:\mathrm{x} \\ $$
Question Number 17714 Answers: 0 Comments: 0
Question Number 17713 Answers: 0 Comments: 2
$$\mathrm{Evaluate}:\:\:\:\:\left(−\sqrt{\mathrm{3}}\right)^{\left(−\sqrt{\mathrm{2}}\right)} \\ $$
Question Number 13249 Answers: 0 Comments: 2
Question Number 13237 Answers: 1 Comments: 2

Question Number 13236 Answers: 0 Comments: 16
Question Number 13234 Answers: 2 Comments: 0
Question Number 13228 Answers: 0 Comments: 5
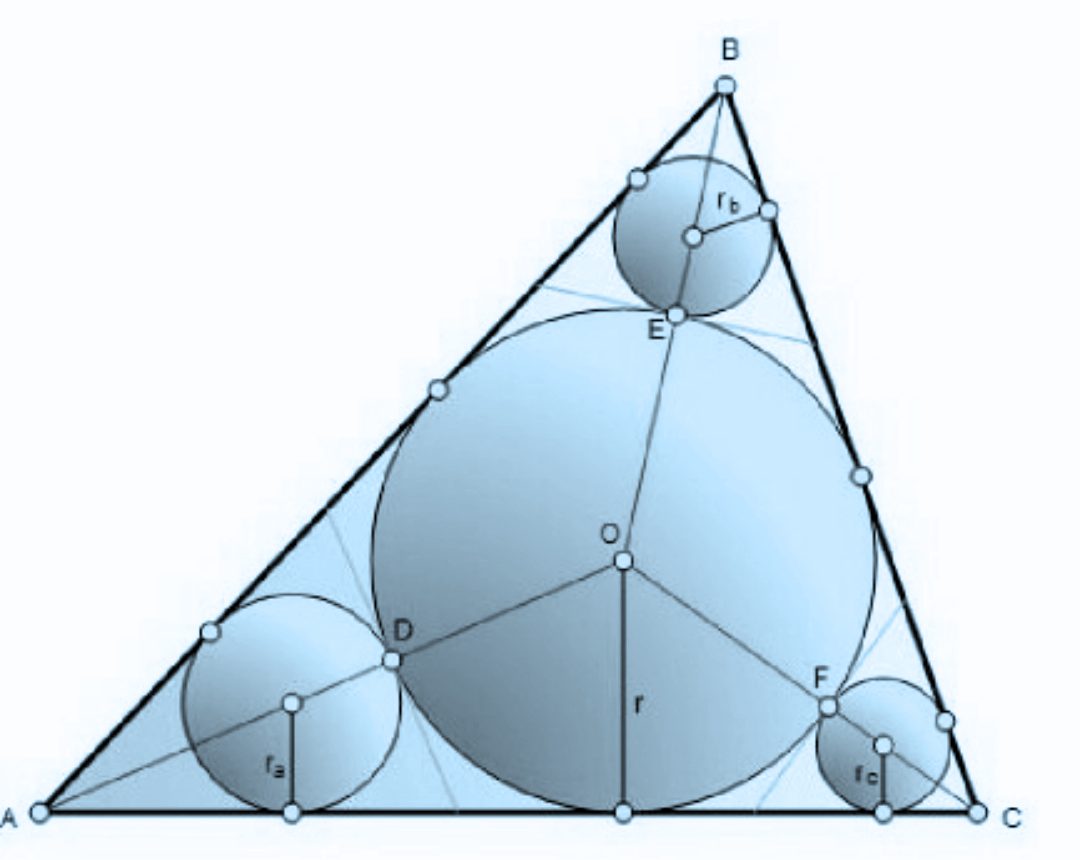
Question Number 13226 Answers: 2 Comments: 0
Question Number 13224 Answers: 1 Comments: 3

Question Number 13206 Answers: 0 Comments: 0
Question Number 13201 Answers: 5 Comments: 1
Question Number 13200 Answers: 2 Comments: 0
Question Number 13194 Answers: 1 Comments: 0

Question Number 13191 Answers: 0 Comments: 4
Question Number 13166 Answers: 2 Comments: 0
Question Number 13155 Answers: 2 Comments: 0

Question Number 13154 Answers: 2 Comments: 0
Question Number 13153 Answers: 1 Comments: 3

Question Number 13152 Answers: 1 Comments: 0
Question Number 13151 Answers: 1 Comments: 0

Question Number 13145 Answers: 1 Comments: 0
Pg 1952 Pg 1953 Pg 1954 Pg 1955 Pg 1956 Pg 1957 Pg 1958 Pg 1959 Pg 1960 Pg 1961
