
AllQuestion and Answers: Page 1956
Question Number 13388 Answers: 0 Comments: 5
Question Number 13377 Answers: 1 Comments: 1

Question Number 13373 Answers: 0 Comments: 4
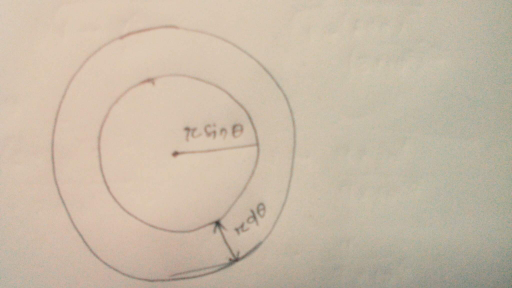
Question Number 13365 Answers: 2 Comments: 0
$$\int\:\:\mathrm{e}^{\left(\mathrm{x}\:+\:\mathrm{e}^{\mathrm{x}} \right)} \:\:\mathrm{dx} \\ $$
Question Number 13364 Answers: 2 Comments: 1
Question Number 13362 Answers: 2 Comments: 0
Question Number 13360 Answers: 1 Comments: 0
Question Number 13359 Answers: 0 Comments: 4
Question Number 13349 Answers: 1 Comments: 0
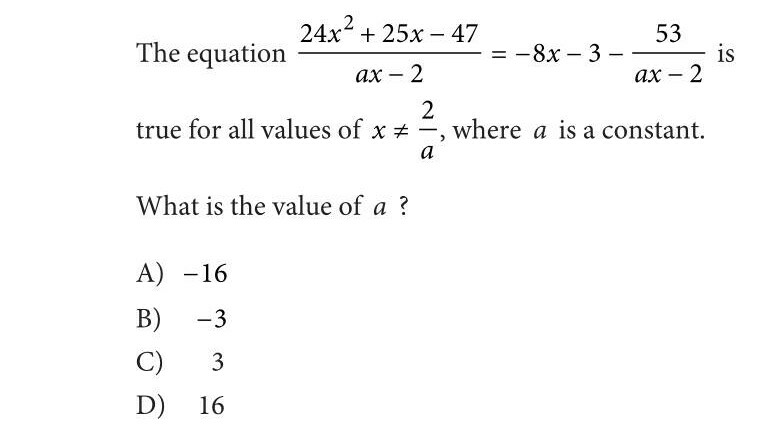
Question Number 13346 Answers: 1 Comments: 2

Question Number 13345 Answers: 0 Comments: 0

Question Number 13336 Answers: 1 Comments: 2
Question Number 13333 Answers: 0 Comments: 5
Question Number 13329 Answers: 0 Comments: 1
Question Number 13328 Answers: 1 Comments: 0
$${Can}\:{we}\:{define}\:{factorial}\:{for}\:{any}\: \\ $$$${real}\:{number}??? \\ $$
Question Number 13327 Answers: 1 Comments: 0
$${how}\:{can}\:{we}\:{expand}\:\left(\mathrm{1}+{x}\right)^{\frac{\mathrm{1}}{\mathrm{2}}} ?? \\ $$
Question Number 13316 Answers: 1 Comments: 0
Question Number 13307 Answers: 1 Comments: 0
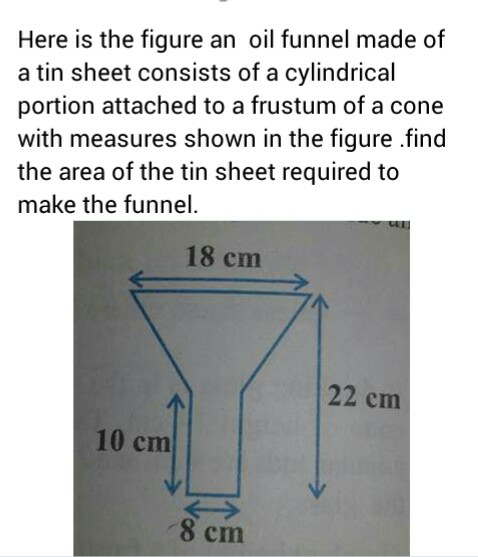
Question Number 13305 Answers: 1 Comments: 0
Question Number 13302 Answers: 2 Comments: 0
Question Number 13888 Answers: 1 Comments: 3
Question Number 13886 Answers: 1 Comments: 0

Question Number 13294 Answers: 0 Comments: 3
Question Number 13283 Answers: 1 Comments: 0
Question Number 13281 Answers: 1 Comments: 0
Question Number 13276 Answers: 0 Comments: 2
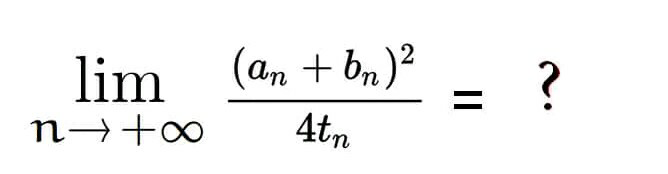
Pg 1951 Pg 1952 Pg 1953 Pg 1954 Pg 1955 Pg 1956 Pg 1957 Pg 1958 Pg 1959 Pg 1960
