
AllQuestion and Answers: Page 1955
Question Number 13578 Answers: 4 Comments: 0

Question Number 13514 Answers: 1 Comments: 21
Question Number 13508 Answers: 1 Comments: 0
Question Number 13501 Answers: 1 Comments: 0
Question Number 13498 Answers: 1 Comments: 1
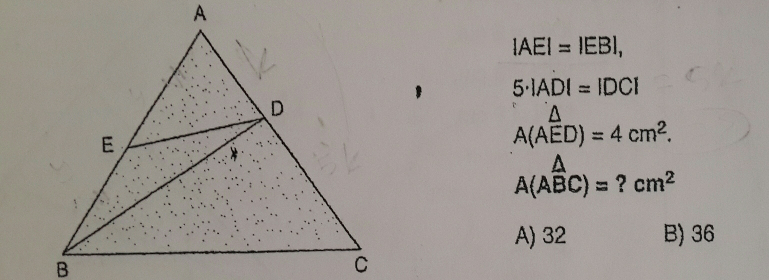
Question Number 13548 Answers: 1 Comments: 11
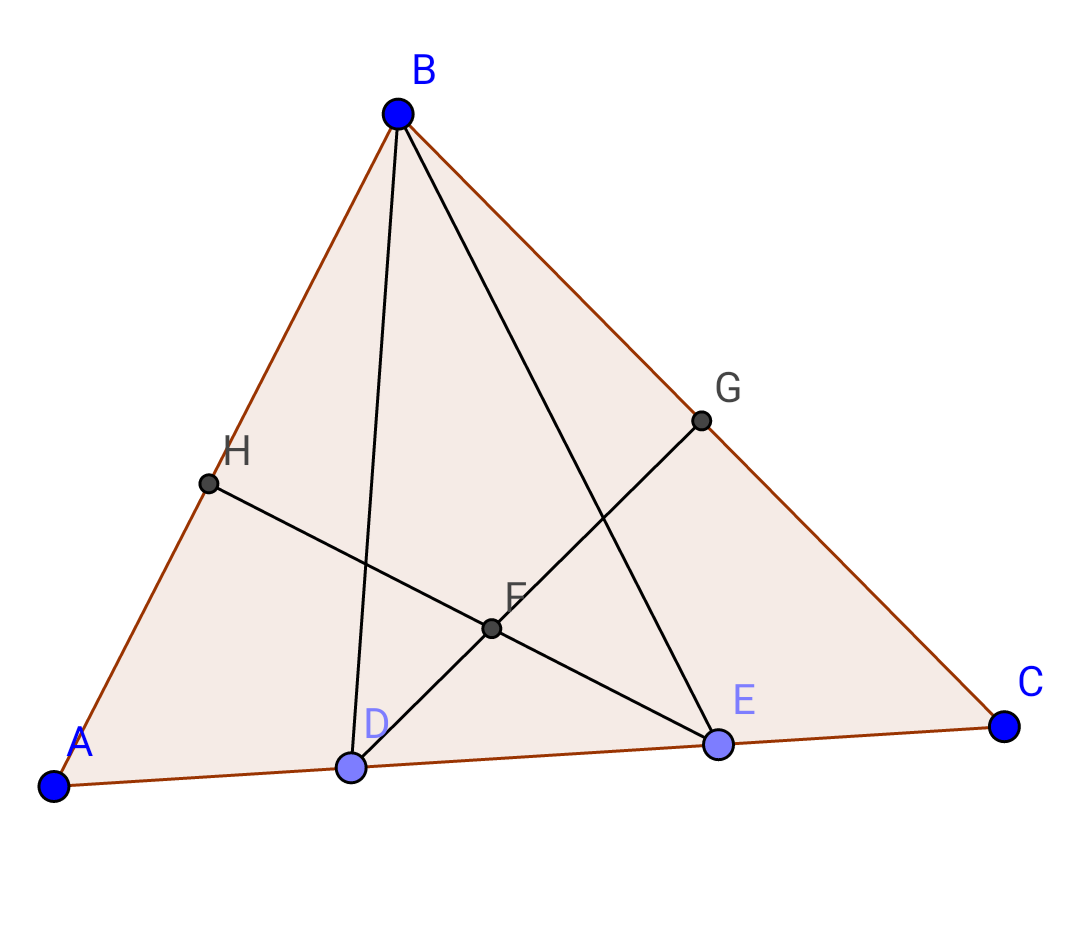
Question Number 13491 Answers: 1 Comments: 0
Question Number 13490 Answers: 1 Comments: 0
Question Number 13478 Answers: 1 Comments: 0
Question Number 13475 Answers: 1 Comments: 0
Question Number 13510 Answers: 1 Comments: 1
Question Number 13449 Answers: 2 Comments: 0
Question Number 13438 Answers: 1 Comments: 0
Question Number 13447 Answers: 0 Comments: 0

Question Number 13434 Answers: 1 Comments: 1
Question Number 13429 Answers: 0 Comments: 2

Question Number 13427 Answers: 0 Comments: 0

Question Number 13412 Answers: 1 Comments: 0
Question Number 13403 Answers: 2 Comments: 2
Question Number 13401 Answers: 1 Comments: 0
Question Number 13395 Answers: 2 Comments: 0
Question Number 13394 Answers: 1 Comments: 0
Question Number 13391 Answers: 1 Comments: 0
Question Number 13389 Answers: 0 Comments: 5
Question Number 13388 Answers: 0 Comments: 5
Question Number 13377 Answers: 1 Comments: 1

Pg 1950 Pg 1951 Pg 1952 Pg 1953 Pg 1954 Pg 1955 Pg 1956 Pg 1957 Pg 1958 Pg 1959
