
AllQuestion and Answers: Page 1950
Question Number 14273 Answers: 1 Comments: 0

Question Number 14269 Answers: 1 Comments: 0
Question Number 14268 Answers: 1 Comments: 0
Question Number 14267 Answers: 1 Comments: 0
Question Number 14246 Answers: 1 Comments: 3

Question Number 14245 Answers: 0 Comments: 0
Question Number 14244 Answers: 1 Comments: 0

Question Number 14219 Answers: 1 Comments: 0

Question Number 14211 Answers: 0 Comments: 11
Question Number 14330 Answers: 0 Comments: 1
Question Number 14215 Answers: 1 Comments: 0

Question Number 14243 Answers: 2 Comments: 0
$$\int\:\left[\mathrm{x}\:\left(\mathrm{lnx}\right)^{\mathrm{2}} \right]\:\mathrm{dx} \\ $$
Question Number 14189 Answers: 2 Comments: 0
Question Number 14181 Answers: 1 Comments: 0
$$\int\:\mathrm{sec}^{\mathrm{6}} \left(\mathrm{x}\right)\:\:\mathrm{dx}\:\: \\ $$
Question Number 14174 Answers: 1 Comments: 0
Question Number 14172 Answers: 0 Comments: 0
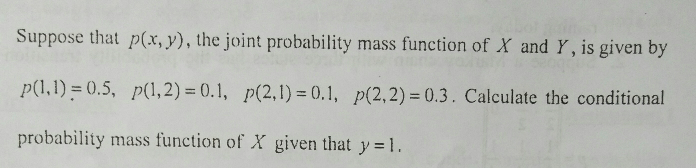
Question Number 14171 Answers: 0 Comments: 0

Question Number 14170 Answers: 0 Comments: 0
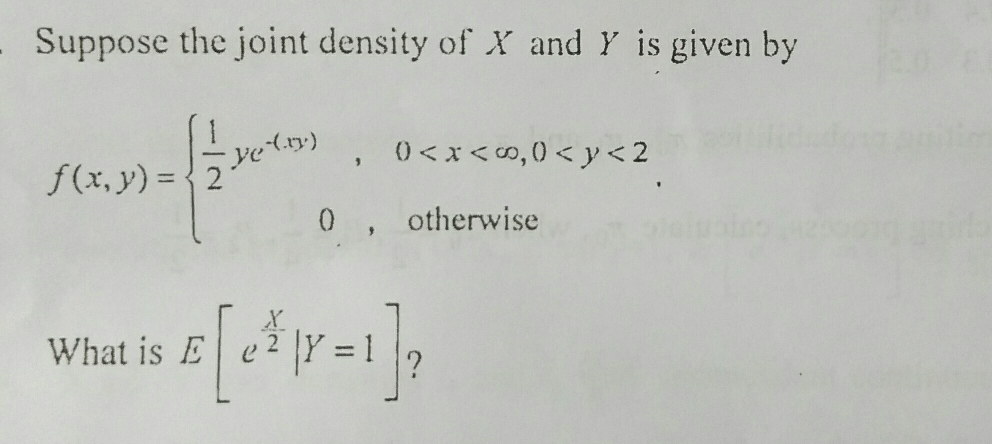
Question Number 14169 Answers: 0 Comments: 0

Question Number 14157 Answers: 2 Comments: 11
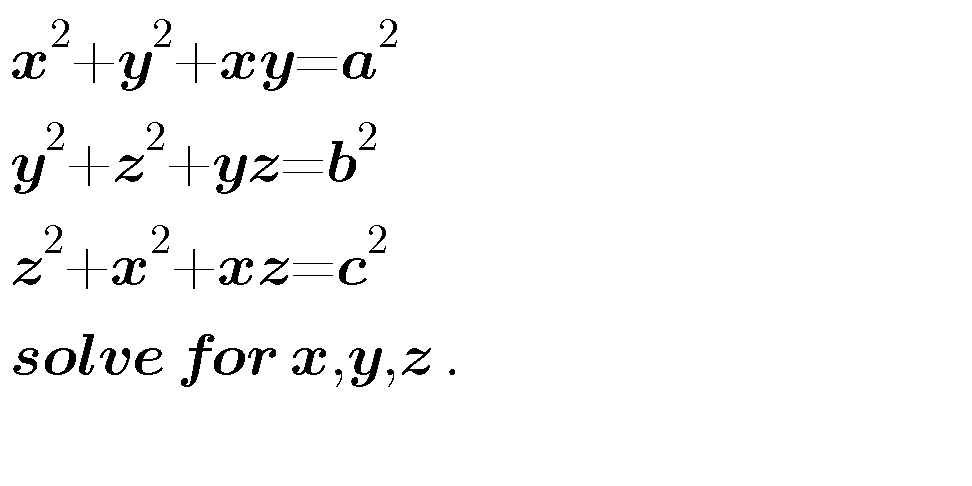
Question Number 14156 Answers: 1 Comments: 0
$$\mathrm{please}\:\mathrm{what}\:\mathrm{does}\:\omega\:\mathrm{mean}? \\ $$
Question Number 14152 Answers: 1 Comments: 0

Question Number 14148 Answers: 2 Comments: 0
Question Number 14147 Answers: 0 Comments: 1
Question Number 14145 Answers: 1 Comments: 1

Question Number 14144 Answers: 1 Comments: 0

Pg 1945 Pg 1946 Pg 1947 Pg 1948 Pg 1949 Pg 1950 Pg 1951 Pg 1952 Pg 1953 Pg 1954
