
AllQuestion and Answers: Page 1943
Question Number 14633 Answers: 3 Comments: 1
Question Number 14632 Answers: 2 Comments: 0
Question Number 14630 Answers: 0 Comments: 2
Question Number 14882 Answers: 0 Comments: 6
Question Number 14879 Answers: 1 Comments: 0
Question Number 14878 Answers: 0 Comments: 3
Question Number 14876 Answers: 0 Comments: 0

Question Number 14614 Answers: 1 Comments: 2
Question Number 14758 Answers: 2 Comments: 4
Question Number 14757 Answers: 1 Comments: 0
Question Number 14759 Answers: 0 Comments: 2
Question Number 14596 Answers: 0 Comments: 3
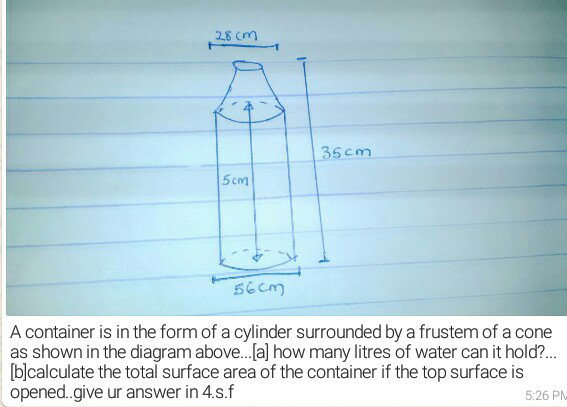
Question Number 14594 Answers: 1 Comments: 0

Question Number 14593 Answers: 1 Comments: 0

Question Number 14592 Answers: 0 Comments: 2

Question Number 14591 Answers: 1 Comments: 0

Question Number 14590 Answers: 1 Comments: 0

Question Number 14572 Answers: 0 Comments: 1
Question Number 14588 Answers: 1 Comments: 0
Question Number 14587 Answers: 1 Comments: 0
Question Number 14564 Answers: 0 Comments: 9
Question Number 14560 Answers: 0 Comments: 0

Question Number 14559 Answers: 1 Comments: 0
Question Number 14544 Answers: 0 Comments: 0

Question Number 14543 Answers: 2 Comments: 1
Question Number 14541 Answers: 0 Comments: 0

Pg 1938 Pg 1939 Pg 1940 Pg 1941 Pg 1942 Pg 1943 Pg 1944 Pg 1945 Pg 1946 Pg 1947
