
AllQuestion and Answers: Page 1941
Question Number 15591 Answers: 1 Comments: 0
Question Number 15578 Answers: 0 Comments: 0
Question Number 15572 Answers: 2 Comments: 1

Question Number 15570 Answers: 2 Comments: 1
$$\mathrm{Solve}:\:\:\:\mathrm{2}^{\mathrm{x}} \:=\:\mathrm{x}^{\mathrm{4}} \\ $$
Question Number 15567 Answers: 2 Comments: 3
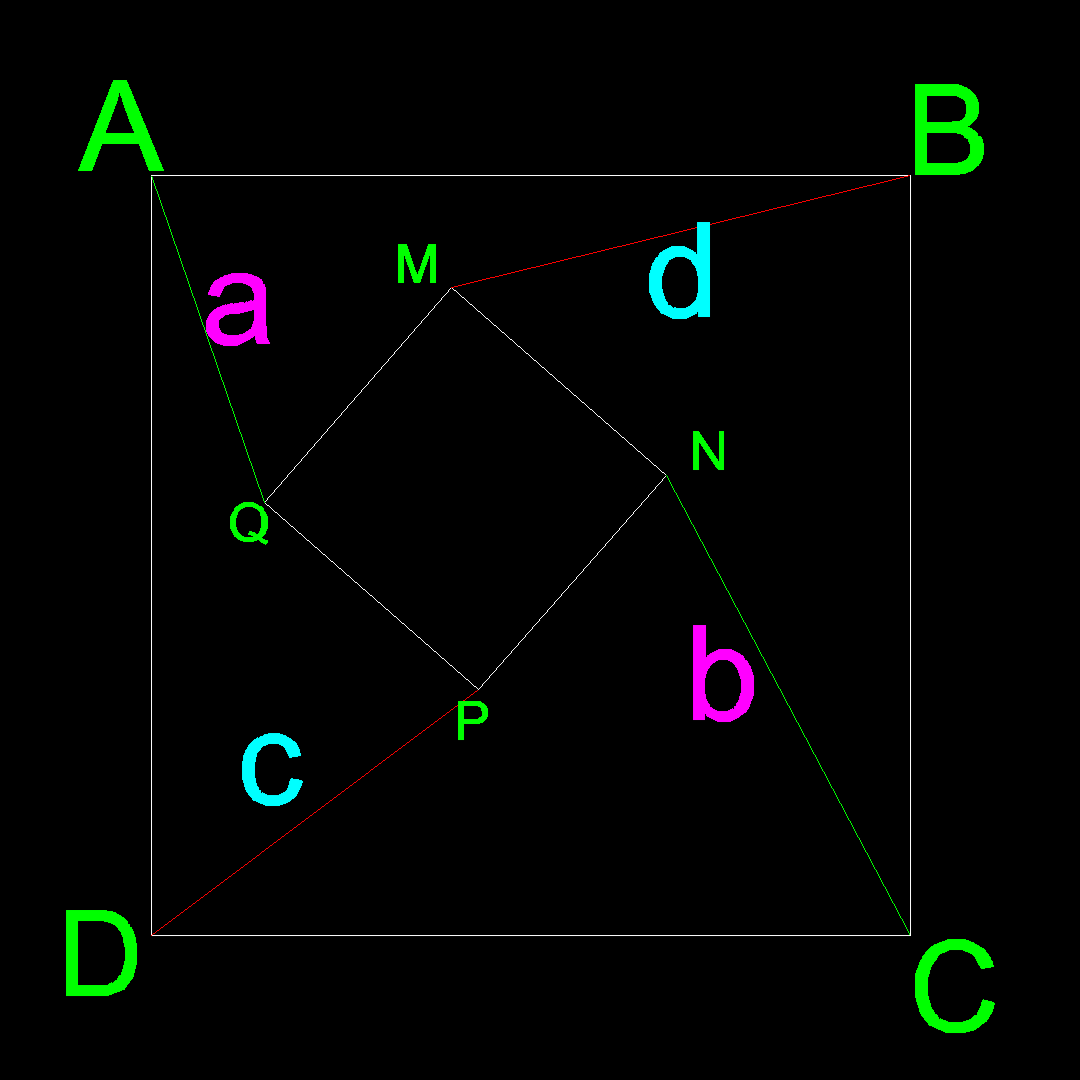
Question Number 15561 Answers: 0 Comments: 3

Question Number 15558 Answers: 1 Comments: 1

Question Number 15555 Answers: 1 Comments: 0
Question Number 15543 Answers: 2 Comments: 0
Question Number 15541 Answers: 0 Comments: 1
Question Number 15539 Answers: 0 Comments: 0

Question Number 15538 Answers: 0 Comments: 0

Question Number 15534 Answers: 1 Comments: 1
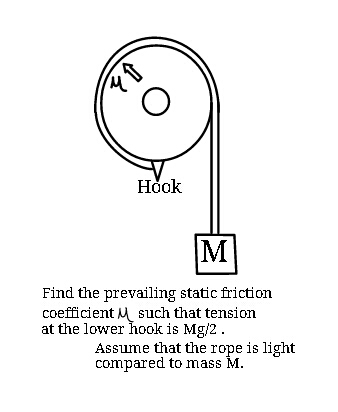
Question Number 15504 Answers: 1 Comments: 3
Question Number 15501 Answers: 1 Comments: 0
$$\mathrm{Solve} \\ $$$${x}^{\mathrm{3}} −\lfloor{x}\rfloor=\mathrm{3} \\ $$
Question Number 15497 Answers: 1 Comments: 5
Question Number 15495 Answers: 0 Comments: 2

Question Number 15485 Answers: 1 Comments: 0

Question Number 15480 Answers: 1 Comments: 1

Question Number 15471 Answers: 1 Comments: 0

Question Number 15470 Answers: 0 Comments: 0

Question Number 15474 Answers: 0 Comments: 0

Question Number 15473 Answers: 0 Comments: 0

Question Number 16613 Answers: 1 Comments: 2

Question Number 15463 Answers: 1 Comments: 0
Question Number 15452 Answers: 1 Comments: 0

Pg 1936 Pg 1937 Pg 1938 Pg 1939 Pg 1940 Pg 1941 Pg 1942 Pg 1943 Pg 1944 Pg 1945
