Question and Answers Forum

AllQuestion and Answers: Page 1939

Question Number 8886 Answers: 1 Comments: 0

solve for β T(h)=T_s −((√π)/2)×(β/ξ)×[erf(ξH)−erf(ξh)]

$${solve}\:{for}\:\beta \\ $$$${T}\left({h}\right)={T}_{{s}} −\frac{\sqrt{\pi}}{\mathrm{2}}×\frac{\beta}{\xi}×\left[{erf}\left(\xi{H}\right)−{erf}\left(\xi{h}\right)\right] \\ $$$$ \\ $$

Question Number 8885 Answers: 1 Comments: 0

Solve simultaneously 2x + y − 2z = 0 ......... (i) 7x + 6y − 9z = 0 ....... (ii) x^3 + y^3 + z^3 = 1728 ...... (iii)

$$\mathrm{Solve}\:\mathrm{simultaneously} \\ $$$$ \\ $$$$\mathrm{2x}\:+\:\mathrm{y}\:−\:\mathrm{2z}\:=\:\mathrm{0}\:.........\:\left(\mathrm{i}\right) \\ $$$$\mathrm{7x}\:+\:\mathrm{6y}\:−\:\mathrm{9z}\:=\:\mathrm{0}\:.......\:\left(\mathrm{ii}\right) \\ $$$$\mathrm{x}^{\mathrm{3}} \:+\:\mathrm{y}^{\mathrm{3}} \:+\:\mathrm{z}^{\mathrm{3}} \:=\:\mathrm{1728}\:\:\:\:......\:\left(\mathrm{iii}\right) \\ $$

Question Number 8884 Answers: 1 Comments: 0

Question Number 8929 Answers: 1 Comments: 1

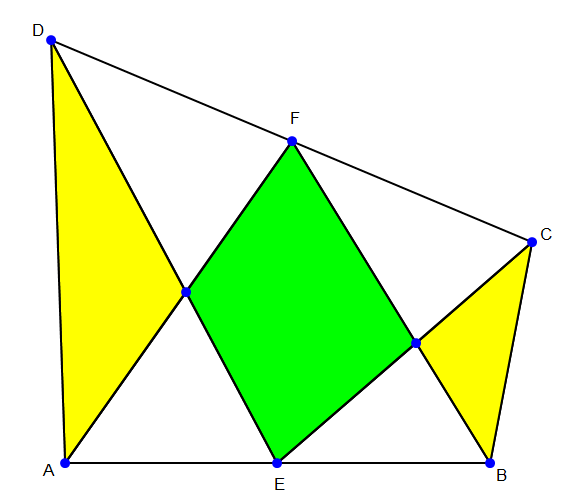
Question Number 8877 Answers: 2 Comments: 3

Question Number 8873 Answers: 1 Comments: 0

simplify 5y^2 × 6x^4

$$\mathrm{simplify}\:\mathrm{5y}^{\mathrm{2}} \:×\:\mathrm{6x}^{\mathrm{4}} \\ $$

Question Number 8870 Answers: 0 Comments: 0

You have n dice. Each dice has p sides, labled 1 to p. What is the probability of rolling k (1≤k≤p)

$$\mathrm{You}\:\mathrm{have}\:{n}\:\mathrm{dice}.\:\mathrm{Each}\:\mathrm{dice}\:\mathrm{has}\:{p}\:\mathrm{sides}, \\ $$$$\mathrm{labled}\:\mathrm{1}\:\mathrm{to}\:{p}.\:\mathrm{What}\:\mathrm{is}\:\mathrm{the}\:\mathrm{probability} \\ $$$$\mathrm{of}\:\mathrm{rolling}\:{k}\:\:\:\:\:\left(\mathrm{1}\leqslant{k}\leqslant{p}\right) \\ $$

Question Number 8868 Answers: 0 Comments: 0

Question Number 8860 Answers: 3 Comments: 1

Question Number 8859 Answers: 1 Comments: 0

If ((tan(α+β−γ))/(tan(a−β+γ)))=((tanγ)/(tanβ)) then show that sin(β−γ)=0 or sin2α+sin2β+sin2Υ=0.

$${If}\:\frac{{tan}\left(\alpha+\beta−\gamma\right)}{{tan}\left({a}−\beta+\gamma\right)}=\frac{{tan}\gamma}{{tan}\beta}\:{then}\:{show} \\ $$$${that}\:{sin}\left(\beta−\gamma\right)=\mathrm{0}\:{or}\:{sin}\mathrm{2}\alpha+{sin}\mathrm{2}\beta+{sin}\mathrm{2}\Upsilon=\mathrm{0}. \\ $$

Question Number 8858 Answers: 1 Comments: 0

Question Number 8853 Answers: 0 Comments: 0

∫_0 ^( n) ((x+1)^(1/x) −1)dx

$$\int_{\mathrm{0}} ^{\:{n}} \left(\left({x}+\mathrm{1}\right)^{\mathrm{1}/{x}} −\mathrm{1}\right){dx} \\ $$

Question Number 8847 Answers: 2 Comments: 5

Question Number 8845 Answers: 0 Comments: 0

Please help me figure out this Quantitative reasoning How did they get this answers. 2,613,400 = 3 2,451,100 = 1 2,541,100 = 2 3,000,001 = 1 3,000,100 = 5 Please help me figure out how they got those answers.

$$\mathrm{Please}\:\mathrm{help}\:\mathrm{me}\:\mathrm{figure}\:\mathrm{out}\:\mathrm{this}\: \\ $$$$\mathrm{Quantitative}\:\mathrm{reasoning} \\ $$$$\mathrm{How}\:\mathrm{did}\:\mathrm{they}\:\mathrm{get}\:\mathrm{this}\:\mathrm{answers}. \\ $$$$ \\ $$$$\mathrm{2},\mathrm{613},\mathrm{400}\:=\:\mathrm{3} \\ $$$$\mathrm{2},\mathrm{451},\mathrm{100}\:=\:\mathrm{1} \\ $$$$\mathrm{2},\mathrm{541},\mathrm{100}\:=\:\mathrm{2} \\ $$$$\mathrm{3},\mathrm{000},\mathrm{001}\:=\:\mathrm{1} \\ $$$$\mathrm{3},\mathrm{000},\mathrm{100}\:=\:\mathrm{5} \\ $$$$ \\ $$$$\mathrm{Please}\:\mathrm{help}\:\mathrm{me}\:\mathrm{figure}\:\mathrm{out}\:\mathrm{how}\:\mathrm{they}\:\mathrm{got}\:\mathrm{those} \\ $$$$\mathrm{answers}. \\ $$

Question Number 8846 Answers: 1 Comments: 0

Let by (a_1 ,a_2 ,...a_n ) we mean LCM of a_1 ,a_2 ,...a_n ,where a_i ∈N. Prove or disprove that ( (a,b),(b,c) )=(a,b,c).

$$\mathrm{Let}\:\mathrm{by}\:\left(\mathrm{a}_{\mathrm{1}} ,\mathrm{a}_{\mathrm{2}} ,...\mathrm{a}_{\mathrm{n}} \right)\:\mathrm{we}\:\mathrm{mean}\:\mathrm{LCM} \\ $$$$\mathrm{of}\:\:\mathrm{a}_{\mathrm{1}} ,\mathrm{a}_{\mathrm{2}} ,...\mathrm{a}_{\mathrm{n}} \:,\mathrm{where}\:\mathrm{a}_{\mathrm{i}} \in\mathbb{N}. \\ $$$$\mathrm{Prove}\:\mathrm{or}\:\mathrm{disprove}\:\mathrm{that}\:\left(\:\left(\mathrm{a},\mathrm{b}\right),\left(\mathrm{b},\mathrm{c}\right)\:\:\right)=\left(\mathrm{a},\mathrm{b},\mathrm{c}\right). \\ $$

Question Number 8839 Answers: 1 Comments: 0

Prove that. lim_(n→∞) (1 + n)^(1/n) = e

$$\mathrm{Prove}\:\mathrm{that}.\: \\ $$$$\underset{\mathrm{n}\rightarrow\infty} {\mathrm{lim}}\:\left(\mathrm{1}\:+\:\mathrm{n}\right)^{\mathrm{1}/\mathrm{n}} \:=\:\mathrm{e} \\ $$

Question Number 8838 Answers: 1 Comments: 0

Show that : e^(iπ + 1) = 0

$$\mathrm{Show}\:\mathrm{that}\::\:\:\mathrm{e}^{\mathrm{i}\pi\:+\:\mathrm{1}} \:=\:\mathrm{0} \\ $$

Question Number 8829 Answers: 0 Comments: 2

The LCM of three whole number is 144. what is their third common multiple.

$$\mathrm{The}\:\mathrm{LCM}\:\mathrm{of}\:\mathrm{three}\:\mathrm{whole}\:\mathrm{number}\:\mathrm{is}\:\mathrm{144}.\: \\ $$$$\mathrm{what}\:\mathrm{is}\:\mathrm{their}\:\mathrm{third}\:\mathrm{common}\:\mathrm{multiple}. \\ $$

Question Number 8828 Answers: 1 Comments: 2

If the third common multiple of two number is 495. Find (a) their LCM (b) the second number if one is 15

$$\mathrm{If}\:\mathrm{the}\:\mathrm{third}\:\mathrm{common}\:\mathrm{multiple}\:\mathrm{of}\:\mathrm{two}\:\mathrm{number} \\ $$$$\mathrm{is}\:\mathrm{495}.\:\mathrm{Find} \\ $$$$\left(\mathrm{a}\right)\:\mathrm{their}\:\mathrm{LCM} \\ $$$$\left(\mathrm{b}\right)\:\mathrm{the}\:\mathrm{second}\:\mathrm{number}\:\mathrm{if}\:\mathrm{one}\:\mathrm{is}\:\mathrm{15} \\ $$

Question Number 8827 Answers: 1 Comments: 1

The LCM of two numbers is 272 and one of them is 16. Find (a) Their second common multiple (b) The other number

$$\mathrm{The}\:\mathrm{LCM}\:\mathrm{of}\:\mathrm{two}\:\mathrm{numbers}\:\mathrm{is}\:\mathrm{272}\:\mathrm{and}\:\mathrm{one}\:\mathrm{of} \\ $$$$\mathrm{them}\:\mathrm{is}\:\mathrm{16}.\:\mathrm{Find} \\ $$$$\left(\mathrm{a}\right)\:\mathrm{Their}\:\mathrm{second}\:\mathrm{common}\:\mathrm{multiple} \\ $$$$\left(\mathrm{b}\right)\:\mathrm{The}\:\mathrm{other}\:\mathrm{number} \\ $$

Question Number 8822 Answers: 0 Comments: 0

Question Number 8823 Answers: 1 Comments: 0

When an electron is placed in an electric field, it experience an electric force whose magnitude is 1.6 times its weight . find the magnitude of the electric field.

$$\mathrm{When}\:\mathrm{an}\:\mathrm{electron}\:\mathrm{is}\:\mathrm{placed}\:\mathrm{in}\:\mathrm{an}\:\mathrm{electric}\:\mathrm{field}, \\ $$$$\mathrm{it}\:\mathrm{experience}\:\mathrm{an}\:\mathrm{electric}\:\mathrm{force}\:\mathrm{whose}\:\mathrm{magnitude} \\ $$$$\mathrm{is}\:\mathrm{1}.\mathrm{6}\:\mathrm{times}\:\mathrm{its}\:\mathrm{weight}\:.\:\mathrm{find}\:\mathrm{the}\:\mathrm{magnitude} \\ $$$$\mathrm{of}\:\mathrm{the}\:\mathrm{electric}\:\mathrm{field}. \\ $$

Question Number 8817 Answers: 0 Comments: 2

If I_1 =∫_( 0) ^(3π) f (cos^2 x)dx and I_2 =∫_( 0) ^π f (cos^2 x)dx then

$$\mathrm{If}\:{I}_{\mathrm{1}} =\underset{\:\mathrm{0}} {\overset{\mathrm{3}\pi} {\int}}\:{f}\:\left(\mathrm{cos}^{\mathrm{2}} {x}\right){dx}\:\mathrm{and}\:\:{I}_{\mathrm{2}} =\underset{\:\mathrm{0}} {\overset{\pi} {\int}}\:{f}\:\left(\mathrm{cos}^{\mathrm{2}} {x}\right){dx} \\ $$$$\mathrm{then} \\ $$

Question Number 8816 Answers: 0 Comments: 0

how can we solve y′′f(x)+y′f_2 (x)=0 y=?

$${how}\:{can}\:{we}\:{solve} \\ $$$${y}''{f}\left({x}\right)+{y}'{f}_{\mathrm{2}} \left({x}\right)=\mathrm{0} \\ $$$${y}=? \\ $$

Question Number 8811 Answers: 0 Comments: 0

Question Number 8808 Answers: 0 Comments: 2

∫_((π/(12)) ) ^(π/4) cos^2 x dx

$$\int_{\frac{\pi}{\mathrm{12}}\:} ^{\frac{\pi}{\mathrm{4}}} \:\mathrm{cos}^{\mathrm{2}} \mathrm{x}\:\:\mathrm{dx} \\ $$

Pg 1934 Pg 1935 Pg 1936 Pg 1937 Pg 1938 Pg 1939 Pg 1940 Pg 1941 Pg 1942 Pg 1943

Contact: info@tinkutara.com