
AllQuestion and Answers: Page 1937
Question Number 16064 Answers: 0 Comments: 8
Question Number 17233 Answers: 0 Comments: 2
Question Number 16354 Answers: 1 Comments: 0
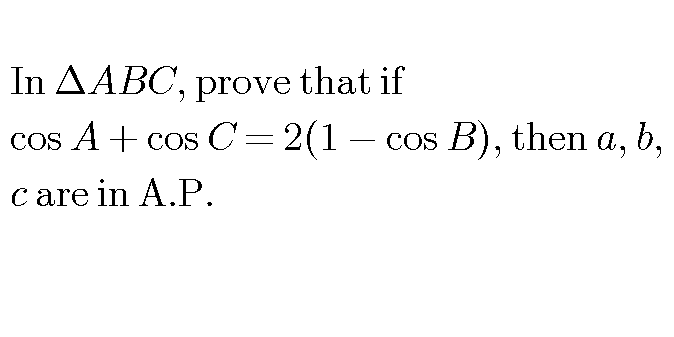
Question Number 16374 Answers: 1 Comments: 0
Question Number 16061 Answers: 1 Comments: 0
$$\int\:{x}^{\mathrm{5}} \sqrt{\mathrm{2}\:−\:{x}^{\mathrm{3}} }\:{dx} \\ $$
Question Number 16057 Answers: 0 Comments: 0
Question Number 16056 Answers: 0 Comments: 0
Question Number 16055 Answers: 1 Comments: 0
Question Number 16053 Answers: 0 Comments: 1
Question Number 16047 Answers: 0 Comments: 1
Question Number 16078 Answers: 0 Comments: 0

Question Number 16044 Answers: 1 Comments: 1
Question Number 16079 Answers: 1 Comments: 1
Question Number 16041 Answers: 1 Comments: 0
Question Number 16039 Answers: 0 Comments: 4

Question Number 16037 Answers: 0 Comments: 1

Question Number 16032 Answers: 0 Comments: 0

Question Number 16029 Answers: 0 Comments: 1
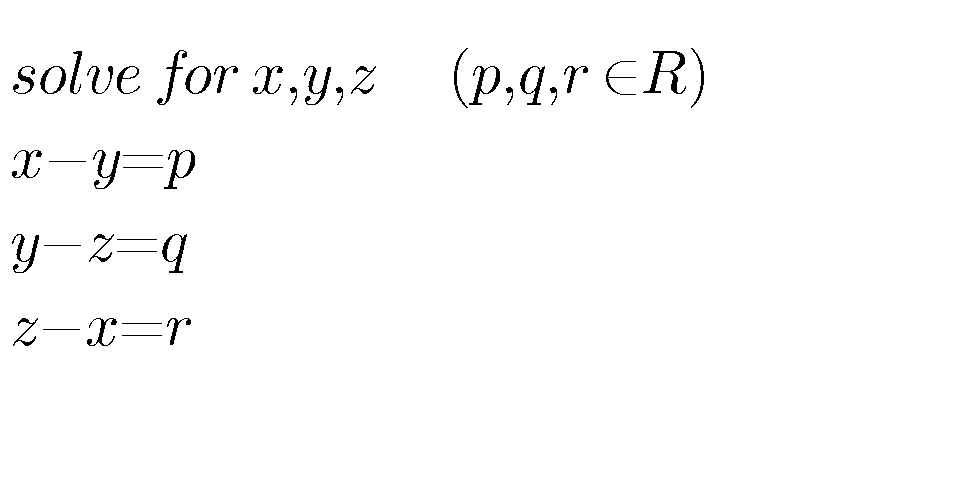
Question Number 16027 Answers: 0 Comments: 0

Question Number 16015 Answers: 1 Comments: 1
Question Number 16014 Answers: 1 Comments: 0
Question Number 16012 Answers: 0 Comments: 2
Question Number 16000 Answers: 2 Comments: 0

Question Number 15999 Answers: 1 Comments: 0
Question Number 15993 Answers: 1 Comments: 1
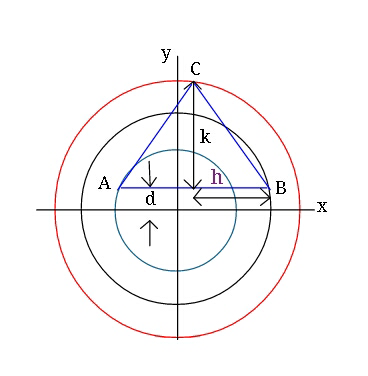
Question Number 15987 Answers: 1 Comments: 1
Pg 1932 Pg 1933 Pg 1934 Pg 1935 Pg 1936 Pg 1937 Pg 1938 Pg 1939 Pg 1940 Pg 1941
