
AllQuestion and Answers: Page 1936
Question Number 15740 Answers: 1 Comments: 0

Question Number 15736 Answers: 1 Comments: 0
Question Number 15721 Answers: 1 Comments: 0
Question Number 15734 Answers: 0 Comments: 3
Question Number 15737 Answers: 0 Comments: 2
Question Number 15707 Answers: 1 Comments: 0
Question Number 15706 Answers: 0 Comments: 2
Question Number 15700 Answers: 1 Comments: 1

Question Number 15699 Answers: 1 Comments: 0
Question Number 15680 Answers: 1 Comments: 0
Question Number 15672 Answers: 1 Comments: 0
Question Number 15671 Answers: 1 Comments: 0
Question Number 15661 Answers: 0 Comments: 6
$$\int\:\frac{\mathrm{sin}\:\mathrm{x}}{\mathrm{x}}\mathrm{dx} \\ $$
Question Number 15656 Answers: 1 Comments: 0
Question Number 15642 Answers: 1 Comments: 0

Question Number 15641 Answers: 1 Comments: 0
Question Number 15667 Answers: 1 Comments: 2

Question Number 15610 Answers: 0 Comments: 3
Question Number 15601 Answers: 0 Comments: 0
Question Number 15599 Answers: 1 Comments: 0
Question Number 15591 Answers: 1 Comments: 0
Question Number 15578 Answers: 0 Comments: 0
Question Number 15572 Answers: 2 Comments: 1

Question Number 15570 Answers: 2 Comments: 1
$$\mathrm{Solve}:\:\:\:\mathrm{2}^{\mathrm{x}} \:=\:\mathrm{x}^{\mathrm{4}} \\ $$
Question Number 15567 Answers: 2 Comments: 3
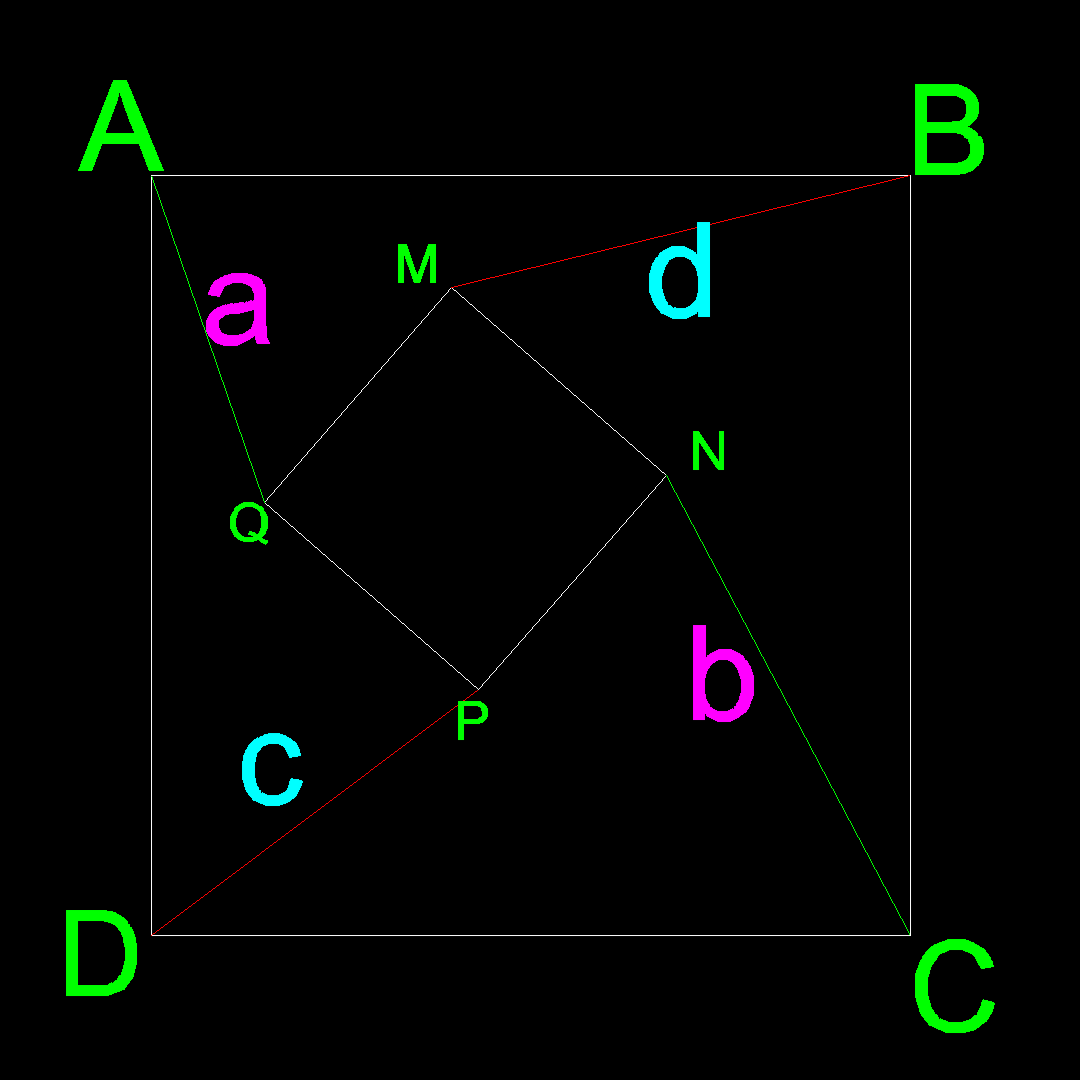
Question Number 15561 Answers: 0 Comments: 3

Pg 1931 Pg 1932 Pg 1933 Pg 1934 Pg 1935 Pg 1936 Pg 1937 Pg 1938 Pg 1939 Pg 1940
