Question and Answers Forum

All Questions   Topic List

AllQuestion and Answers: Page 1935

Question Number 15943    Answers: 0   Comments: 0

Solve: x(dy/dx) + 3y = 3x^x y^(2/3)

$$\mathrm{Solve}: \\ $$$$\mathrm{x}\frac{\mathrm{dy}}{\mathrm{dx}}\:+\:\mathrm{3y}\:=\:\mathrm{3x}^{\mathrm{x}} \:\mathrm{y}^{\mathrm{2}/\mathrm{3}} \\ $$

Question Number 15942    Answers: 1   Comments: 0

Help. solve(x+2)dy/dx=3−2y/x

$$\mathrm{Help}. \\ $$$$\mathrm{solve}\left(\mathrm{x}+\mathrm{2}\right)\mathrm{dy}/\mathrm{dx}=\mathrm{3}−\mathrm{2y}/\mathrm{x} \\ $$

Question Number 15932    Answers: 1   Comments: 1

A particle is projected from the foot of an inclined plane having inclination 45°, with the velocity u at an angle θ (> 45°) with the horizontal in a vertical plane containing the line of greatest slope through the point of projection. Find the value of tan θ if the particle strikes the plane (i) Horizontally (ii) Normally

$$\mathrm{A}\:\mathrm{particle}\:\mathrm{is}\:\mathrm{projected}\:\mathrm{from}\:\mathrm{the}\:\mathrm{foot}\:\mathrm{of} \\ $$$$\mathrm{an}\:\mathrm{inclined}\:\mathrm{plane}\:\mathrm{having}\:\mathrm{inclination} \\ $$$$\mathrm{45}°,\:\mathrm{with}\:\mathrm{the}\:\mathrm{velocity}\:{u}\:\mathrm{at}\:\mathrm{an}\:\mathrm{angle}\:\theta \\ $$$$\left(>\:\mathrm{45}°\right)\:\mathrm{with}\:\mathrm{the}\:\mathrm{horizontal}\:\mathrm{in}\:\mathrm{a}\:\mathrm{vertical} \\ $$$$\mathrm{plane}\:\mathrm{containing}\:\mathrm{the}\:\mathrm{line}\:\mathrm{of}\:\mathrm{greatest} \\ $$$$\mathrm{slope}\:\mathrm{through}\:\mathrm{the}\:\mathrm{point}\:\mathrm{of}\:\mathrm{projection}. \\ $$$$\mathrm{Find}\:\mathrm{the}\:\mathrm{value}\:\mathrm{of}\:\mathrm{tan}\:\theta\:\mathrm{if}\:\mathrm{the}\:\mathrm{particle} \\ $$$$\mathrm{strikes}\:\mathrm{the}\:\mathrm{plane} \\ $$$$\left(\mathrm{i}\right)\:\mathrm{Horizontally} \\ $$$$\left(\mathrm{ii}\right)\:\mathrm{Normally} \\ $$

Question Number 15939    Answers: 0   Comments: 1

Question Number 15927    Answers: 0   Comments: 5

Question Number 15919    Answers: 0   Comments: 1

multiply 3x+4y+5x−8y

$${multiply}\:\mathrm{3}{x}+\mathrm{4}{y}+\mathrm{5}{x}−\mathrm{8}{y} \\ $$

Question Number 15917    Answers: 1   Comments: 1

Question Number 15916    Answers: 2   Comments: 2

Question Number 15908    Answers: 1   Comments: 7

Question Number 15906    Answers: 1   Comments: 0

If λ_1 and λ_2 are respectively the wavelengths of the series limit of Lyman and Balmer series of Hydrogen atom, then the wavelength of the first line of the Lyman series of the H-atom is (1) λ_1 − λ_2 (2) (√(λ_1 λ_2 )) (3) ((λ_2 − λ_1 )/(λ_1 λ_2 )) (4) ((λ_1 λ_2 )/(λ_2 − λ_1 ))

$$\mathrm{If}\:\lambda_{\mathrm{1}} \:\mathrm{and}\:\lambda_{\mathrm{2}} \:\mathrm{are}\:\mathrm{respectively}\:\mathrm{the} \\ $$$$\mathrm{wavelengths}\:\mathrm{of}\:\mathrm{the}\:\mathrm{series}\:\mathrm{limit}\:\mathrm{of}\:\mathrm{Lyman} \\ $$$$\mathrm{and}\:\mathrm{Balmer}\:\mathrm{series}\:\mathrm{of}\:\mathrm{Hydrogen}\:\mathrm{atom}, \\ $$$$\mathrm{then}\:\mathrm{the}\:\mathrm{wavelength}\:\mathrm{of}\:\mathrm{the}\:\mathrm{first}\:\mathrm{line}\:\mathrm{of} \\ $$$$\mathrm{the}\:\mathrm{Lyman}\:\mathrm{series}\:\mathrm{of}\:\mathrm{the}\:\mathrm{H}-\mathrm{atom}\:\mathrm{is} \\ $$$$\left(\mathrm{1}\right)\:\lambda_{\mathrm{1}} \:−\:\lambda_{\mathrm{2}} \\ $$$$\left(\mathrm{2}\right)\:\sqrt{\lambda_{\mathrm{1}} \lambda_{\mathrm{2}} } \\ $$$$\left(\mathrm{3}\right)\:\frac{\lambda_{\mathrm{2}} \:−\:\lambda_{\mathrm{1}} }{\lambda_{\mathrm{1}} \lambda_{\mathrm{2}} } \\ $$$$\left(\mathrm{4}\right)\:\frac{\lambda_{\mathrm{1}} \lambda_{\mathrm{2}} }{\lambda_{\mathrm{2}} \:−\:\lambda_{\mathrm{1}} } \\ $$

Question Number 15904    Answers: 2   Comments: 1

Question Number 15894    Answers: 0   Comments: 2

If the angles of a triangle ABC be in A.P., then (1) c^2 = a^2 + b^2 − ab (2) b^2 = a^2 + c^2 − ac (3) a^2 = b^2 + c^2 − ac (4) b^2 = a^2 + c^2

$$\mathrm{If}\:\mathrm{the}\:\mathrm{angles}\:\mathrm{of}\:\mathrm{a}\:\mathrm{triangle}\:{ABC}\:\mathrm{be}\:\mathrm{in} \\ $$$$\mathrm{A}.\mathrm{P}.,\:\mathrm{then} \\ $$$$\left(\mathrm{1}\right)\:{c}^{\mathrm{2}} \:=\:{a}^{\mathrm{2}} \:+\:{b}^{\mathrm{2}} \:−\:{ab} \\ $$$$\left(\mathrm{2}\right)\:{b}^{\mathrm{2}} \:=\:{a}^{\mathrm{2}} \:+\:{c}^{\mathrm{2}} \:−\:{ac} \\ $$$$\left(\mathrm{3}\right)\:{a}^{\mathrm{2}} \:=\:{b}^{\mathrm{2}} \:+\:{c}^{\mathrm{2}} \:−\:{ac} \\ $$$$\left(\mathrm{4}\right)\:{b}^{\mathrm{2}} \:=\:{a}^{\mathrm{2}} \:+\:{c}^{\mathrm{2}} \\ $$

Question Number 15891    Answers: 0   Comments: 0

Find out last odd digit in the expansion of 1000!

$$\mathrm{Find}\:\mathrm{out}\:\boldsymbol{\mathrm{last}}\:\boldsymbol{\mathrm{odd}}\:\boldsymbol{\mathrm{digit}}\:\mathrm{in}\:\mathrm{the} \\ $$$$\mathrm{expansion}\:\mathrm{of}\:\mathrm{1000}! \\ $$

Question Number 15889    Answers: 0   Comments: 0

Find out first non-five digit from right in the expansion of (1×3×5×...×625).

$$\mathrm{Find}\:\mathrm{out}\:\boldsymbol{\mathrm{first}}\:\boldsymbol{\mathrm{non}}-\boldsymbol{\mathrm{five}}\:\boldsymbol{\mathrm{digit}}\:\mathrm{from}\:\mathrm{right} \\ $$$$\mathrm{in}\:\mathrm{the}\:\mathrm{expansion}\:\mathrm{of}\:\left(\mathrm{1}×\mathrm{3}×\mathrm{5}×...×\mathrm{625}\right). \\ $$

Question Number 15888    Answers: 1   Comments: 0

Prove that in ΔABC, a^3 cos (B − C) + b^3 cos (C − A) + c^3 cos (A − B) = 3abc

$$\mathrm{Prove}\:\mathrm{that}\:\mathrm{in}\:\Delta{ABC},\:{a}^{\mathrm{3}} \:\mathrm{cos}\:\left({B}\:−\:{C}\right)\:+ \\ $$$${b}^{\mathrm{3}} \:\mathrm{cos}\:\left({C}\:−\:{A}\right)\:+\:{c}^{\mathrm{3}} \:\mathrm{cos}\:\left({A}\:−\:{B}\right)\:=\:\mathrm{3}{abc} \\ $$

Question Number 15893    Answers: 1   Comments: 0

In ΔABC, sides a, b, c are roots of the equation x^3 − px^2 + qx − r = 0. Prove that area of ΔABC is (1/4)(√(p(4pq − p^3 − 8r)))

$$\mathrm{In}\:\Delta{ABC},\:\mathrm{sides}\:{a},\:{b},\:{c}\:\mathrm{are}\:\mathrm{roots}\:\mathrm{of}\:\mathrm{the} \\ $$$$\mathrm{equation}\:{x}^{\mathrm{3}} \:−\:{px}^{\mathrm{2}} \:+\:{qx}\:−\:{r}\:=\:\mathrm{0}.\:\mathrm{Prove} \\ $$$$\mathrm{that}\:\mathrm{area}\:\mathrm{of}\:\Delta{ABC}\:\mathrm{is} \\ $$$$\frac{\mathrm{1}}{\mathrm{4}}\sqrt{{p}\left(\mathrm{4}{pq}\:−\:{p}^{\mathrm{3}} \:−\:\mathrm{8}{r}\right)} \\ $$

Question Number 15881    Answers: 1   Comments: 1

Question Number 15880    Answers: 2   Comments: 0

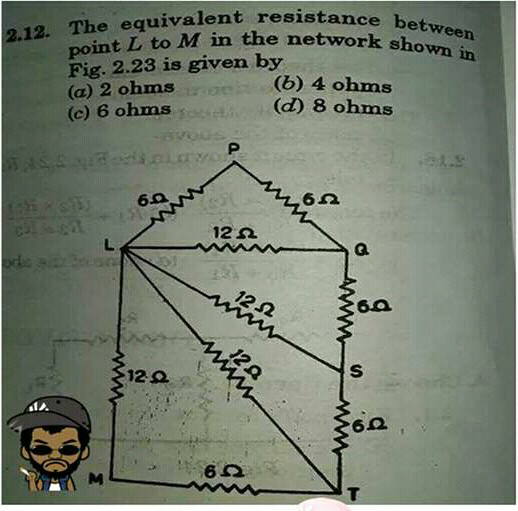
Question Number 15869    Answers: 1   Comments: 1

If ax^2 +(b/x)≥c for all x,a,b>0 then prove minimum value of 27ab^2 is 4c^2 .

$$\mathrm{If}\:{ax}^{\mathrm{2}} +\frac{{b}}{{x}}\geqslant{c}\:\mathrm{for}\:\mathrm{all}\:{x},{a},{b}>\mathrm{0}\:\mathrm{then} \\ $$$$\mathrm{prove}\:\mathrm{minimum}\:\mathrm{value}\:\mathrm{of} \\ $$$$\mathrm{27}{ab}^{\mathrm{2}} \:\mathrm{is}\:\mathrm{4}{c}^{\mathrm{2}} . \\ $$

Question Number 15868    Answers: 1   Comments: 0

Find the equation and radius of the circumcircle of the triangle formed by the three line: 2y − 9x + 26 = 0 9y + 2x + 32 = 0 11y − 7x − 27 = 0

$$\mathrm{Find}\:\mathrm{the}\:\mathrm{equation}\:\mathrm{and}\:\mathrm{radius}\:\mathrm{of}\:\mathrm{the}\:\mathrm{circumcircle}\:\mathrm{of}\:\mathrm{the}\:\mathrm{triangle}\:\mathrm{formed}\:\mathrm{by}\: \\ $$$$\mathrm{the}\:\mathrm{three}\:\mathrm{line}: \\ $$$$\mathrm{2y}\:−\:\mathrm{9x}\:+\:\mathrm{26}\:=\:\mathrm{0} \\ $$$$\mathrm{9y}\:+\:\mathrm{2x}\:+\:\mathrm{32}\:=\:\mathrm{0} \\ $$$$\mathrm{11y}\:−\:\mathrm{7x}\:−\:\mathrm{27}\:=\:\mathrm{0} \\ $$

Question Number 15865    Answers: 2   Comments: 0

a,b,c∈R^(+ ) andIf a+b+c=18 then maximum value of a^2 b^3 c^4 is

$${a},{b},{c}\in\mathbb{R}^{+\:} \mathrm{andIf}\:{a}+{b}+{c}=\mathrm{18}\:\mathrm{then}\:\mathrm{maximum}\:\mathrm{value} \\ $$$$\mathrm{of}\:{a}^{\mathrm{2}} {b}^{\mathrm{3}} {c}^{\mathrm{4}} \:\mathrm{is} \\ $$

Question Number 15856    Answers: 1   Comments: 0

A particle is moving along a straight line with uniform acceleration has velocities 7 m/s at P and 17 m/s at Q. If R is the midpoint of PQ, then the average velocity between P and R is?

$$\mathrm{A}\:\mathrm{particle}\:\mathrm{is}\:\mathrm{moving}\:\mathrm{along}\:\mathrm{a}\:\mathrm{straight} \\ $$$$\mathrm{line}\:\mathrm{with}\:\mathrm{uniform}\:\mathrm{acceleration}\:\mathrm{has} \\ $$$$\mathrm{velocities}\:\mathrm{7}\:\mathrm{m}/\mathrm{s}\:\mathrm{at}\:{P}\:\mathrm{and}\:\mathrm{17}\:\mathrm{m}/\mathrm{s}\:\mathrm{at}\:{Q}. \\ $$$$\mathrm{If}\:{R}\:\mathrm{is}\:\mathrm{the}\:\mathrm{midpoint}\:\mathrm{of}\:{PQ},\:\mathrm{then}\:\mathrm{the} \\ $$$$\mathrm{average}\:\mathrm{velocity}\:\mathrm{between}\:{P}\:\mathrm{and}\:{R}\:\mathrm{is}? \\ $$

Question Number 15850    Answers: 0   Comments: 0

Let (X, T) be any topological space . Verify that the intersection of any finite number of members of T is a member of T. Use mathematical induction to prove your result.

$$\mathrm{Let}\:\left(\mathrm{X},\:\mathrm{T}\right)\:\mathrm{be}\:\mathrm{any}\:\mathrm{topological}\:\mathrm{space}\:.\:\mathrm{Verify}\:\mathrm{that}\:\mathrm{the}\:\mathrm{intersection}\:\mathrm{of}\:\mathrm{any}\: \\ $$$$\mathrm{finite}\:\mathrm{number}\:\mathrm{of}\:\mathrm{members}\:\mathrm{of}\:\mathrm{T}\:\mathrm{is}\:\mathrm{a}\:\mathrm{member}\:\mathrm{of}\:\mathrm{T}.\:\mathrm{Use}\:\mathrm{mathematical} \\ $$$$\mathrm{induction}\:\mathrm{to}\:\mathrm{prove}\:\mathrm{your}\:\mathrm{result}. \\ $$

Question Number 15840    Answers: 1   Comments: 2

Solve the ODE (dy/dx) + x^2 y = x^4

$$\mathrm{Solve}\:\mathrm{the}\:\:\mathrm{ODE} \\ $$$$\frac{\mathrm{dy}}{\mathrm{dx}}\:+\:\mathrm{x}^{\mathrm{2}} \mathrm{y}\:=\:\mathrm{x}^{\mathrm{4}} \\ $$$$ \\ $$

Question Number 15839    Answers: 0   Comments: 1

Question Number 15835    Answers: 0   Comments: 1

Number of decimal digits in 50! is

$$\:\mathrm{Number}\:\mathrm{of}\: \\ $$$$\mathrm{decimal}\:\:\mathrm{digits}\: \\ $$$$\mathrm{in}\:\:\mathrm{50}!\:\mathrm{is} \\ $$

  Pg 1930      Pg 1931      Pg 1932      Pg 1933      Pg 1934      Pg 1935      Pg 1936      Pg 1937      Pg 1938      Pg 1939   

Terms of Service

Privacy Policy

Contact: info@tinkutara.com