
AllQuestion and Answers: Page 1934
Question Number 16012 Answers: 0 Comments: 2
Question Number 16000 Answers: 2 Comments: 0

Question Number 15999 Answers: 1 Comments: 0
Question Number 15993 Answers: 1 Comments: 1
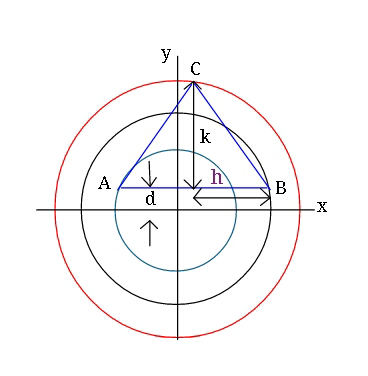
Question Number 15987 Answers: 1 Comments: 1
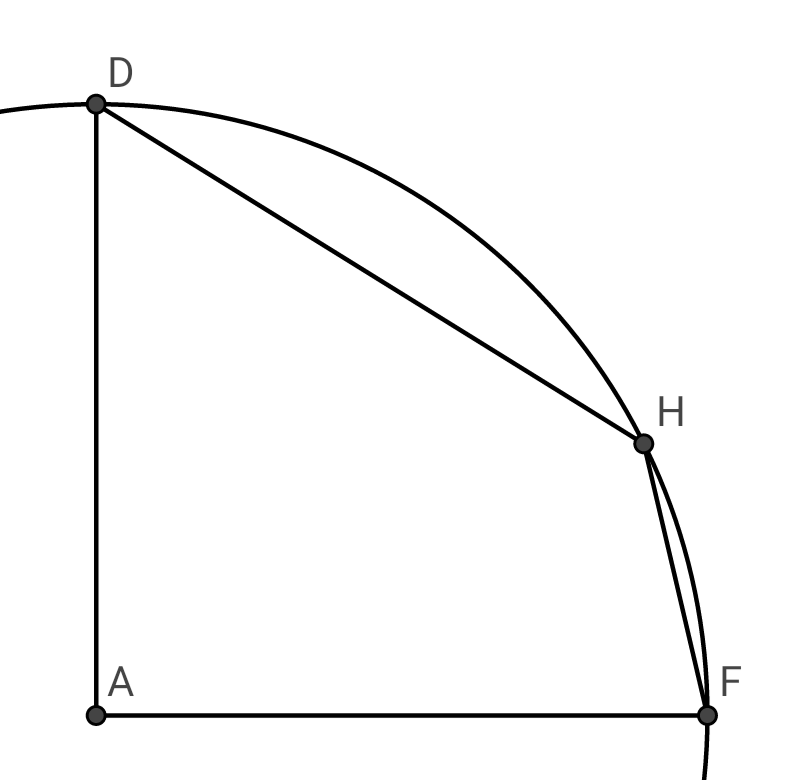
Question Number 15982 Answers: 0 Comments: 3
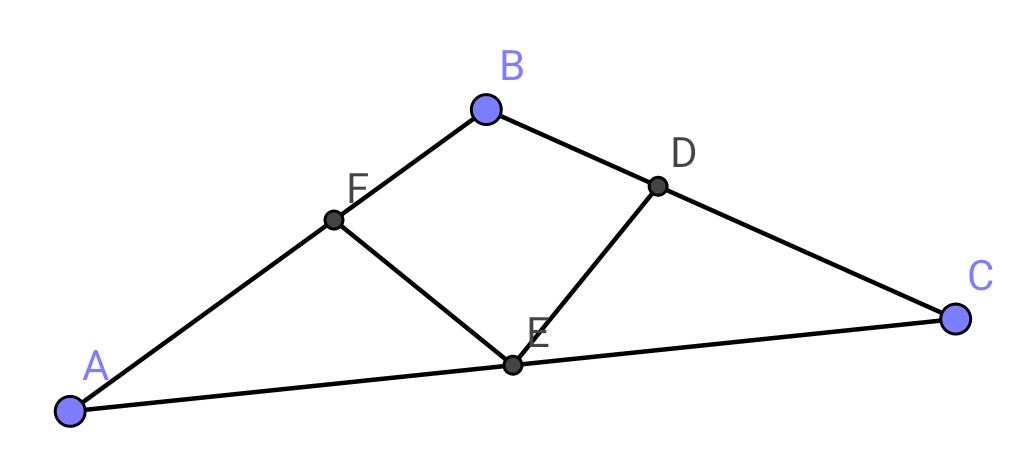
Question Number 15975 Answers: 1 Comments: 1
Question Number 15972 Answers: 0 Comments: 1
$$\int\mathrm{tan}^{\mathrm{2}} \mathrm{x}\:\mathrm{sec}\:\mathrm{x}\:\mathrm{dx}\: \\ $$
Question Number 15971 Answers: 0 Comments: 1
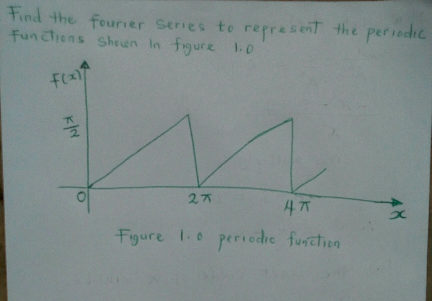
Question Number 15969 Answers: 0 Comments: 17

Question Number 15967 Answers: 1 Comments: 1
Question Number 15961 Answers: 0 Comments: 5
Question Number 15955 Answers: 0 Comments: 2
Question Number 15948 Answers: 1 Comments: 1

Question Number 15943 Answers: 0 Comments: 0
Question Number 15942 Answers: 1 Comments: 0
Question Number 15932 Answers: 1 Comments: 1
Question Number 15939 Answers: 0 Comments: 1

Question Number 15927 Answers: 0 Comments: 5

Question Number 15919 Answers: 0 Comments: 1
$${multiply}\:\mathrm{3}{x}+\mathrm{4}{y}+\mathrm{5}{x}−\mathrm{8}{y} \\ $$
Question Number 15917 Answers: 1 Comments: 1

Question Number 15916 Answers: 2 Comments: 2

Question Number 15908 Answers: 1 Comments: 7

Question Number 15906 Answers: 1 Comments: 0
Question Number 15904 Answers: 2 Comments: 1

Question Number 15894 Answers: 0 Comments: 2
Pg 1929 Pg 1930 Pg 1931 Pg 1932 Pg 1933 Pg 1934 Pg 1935 Pg 1936 Pg 1937 Pg 1938
