
AllQuestion and Answers: Page 1931
Question Number 16330 Answers: 0 Comments: 0

Question Number 16310 Answers: 1 Comments: 3

Question Number 16302 Answers: 1 Comments: 5
Question Number 16294 Answers: 1 Comments: 1
Question Number 16281 Answers: 0 Comments: 0
Question Number 16277 Answers: 3 Comments: 1
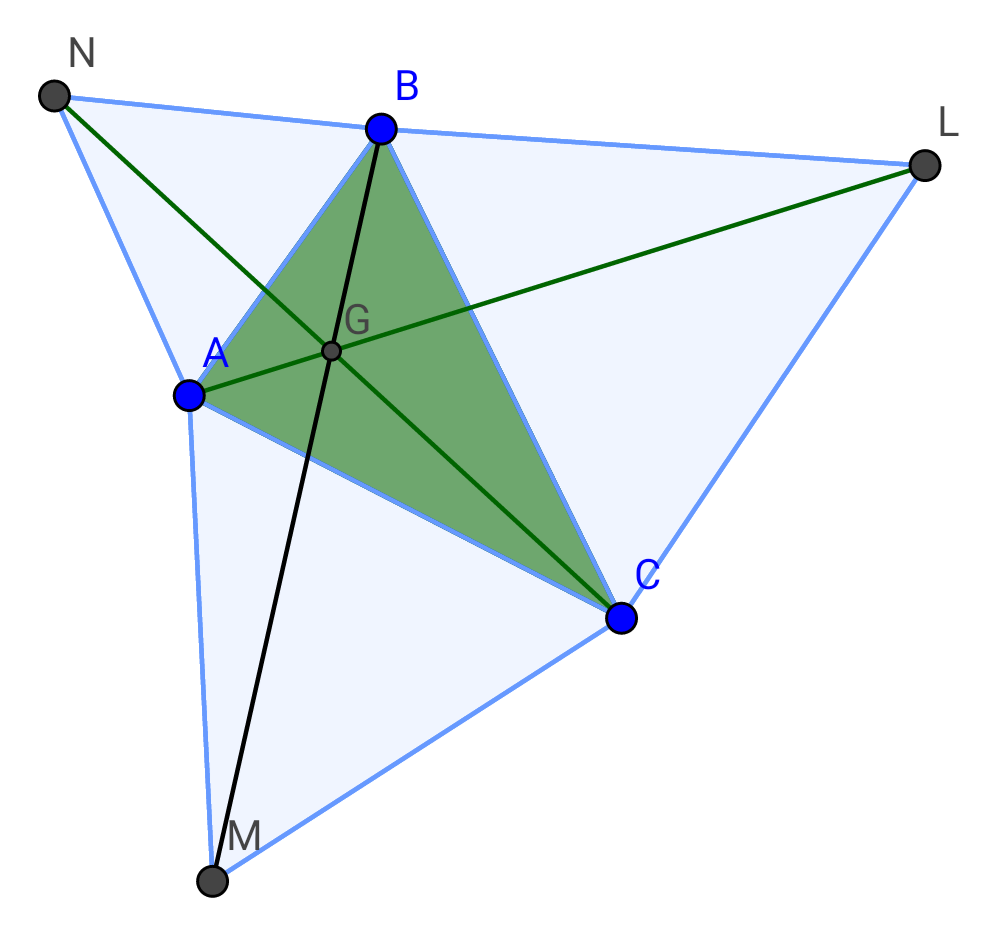
Question Number 16273 Answers: 2 Comments: 4
Question Number 16271 Answers: 1 Comments: 0
Question Number 16269 Answers: 1 Comments: 0
Question Number 16240 Answers: 2 Comments: 1

Question Number 16238 Answers: 0 Comments: 0
Question Number 16226 Answers: 0 Comments: 1
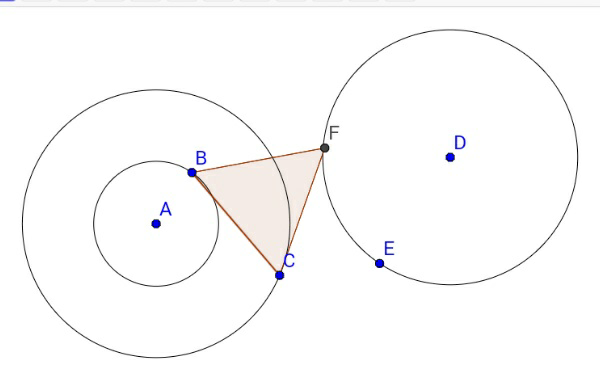
Question Number 16220 Answers: 1 Comments: 0
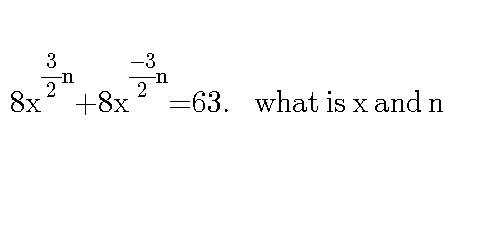
Question Number 16214 Answers: 2 Comments: 4
Question Number 16194 Answers: 0 Comments: 21

Question Number 16179 Answers: 1 Comments: 0
Question Number 16616 Answers: 1 Comments: 1
Question Number 16156 Answers: 0 Comments: 2
Question Number 16155 Answers: 1 Comments: 0
Question Number 16153 Answers: 1 Comments: 0
Question Number 16152 Answers: 1 Comments: 0
Question Number 16150 Answers: 1 Comments: 1
Question Number 16140 Answers: 2 Comments: 0

Question Number 16139 Answers: 2 Comments: 0
Question Number 16138 Answers: 0 Comments: 0
Question Number 16137 Answers: 0 Comments: 0
Pg 1926 Pg 1927 Pg 1928 Pg 1929 Pg 1930 Pg 1931 Pg 1932 Pg 1933 Pg 1934 Pg 1935
