
AllQuestion and Answers: Page 1921
Question Number 17497 Answers: 1 Comments: 0
$$\mathrm{Evaluate}:\:\:\:\mathrm{sin}\left(\mathrm{9}\right)° \\ $$
Question Number 17481 Answers: 0 Comments: 0

Question Number 17480 Answers: 1 Comments: 0
Question Number 17475 Answers: 1 Comments: 0
Question Number 17473 Answers: 1 Comments: 0
Question Number 17472 Answers: 1 Comments: 0
Question Number 17479 Answers: 0 Comments: 0
Question Number 17449 Answers: 1 Comments: 4
Question Number 17492 Answers: 1 Comments: 0
Question Number 17446 Answers: 0 Comments: 2
Question Number 17444 Answers: 1 Comments: 0
Question Number 17440 Answers: 1 Comments: 0
Question Number 17645 Answers: 2 Comments: 1
Question Number 17438 Answers: 0 Comments: 0
Question Number 17435 Answers: 1 Comments: 0
Question Number 17421 Answers: 1 Comments: 0
Question Number 17420 Answers: 1 Comments: 0
Question Number 17454 Answers: 1 Comments: 0
Question Number 17401 Answers: 0 Comments: 4
Question Number 17397 Answers: 1 Comments: 0

Question Number 17393 Answers: 1 Comments: 0
Question Number 17392 Answers: 2 Comments: 0
Question Number 17391 Answers: 1 Comments: 0
Question Number 17377 Answers: 1 Comments: 0
Question Number 17374 Answers: 1 Comments: 1
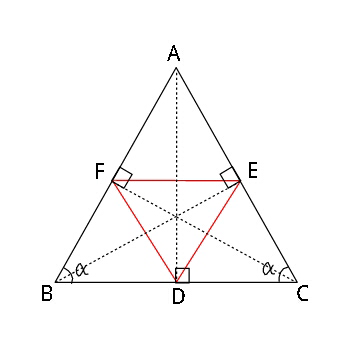
Question Number 17373 Answers: 2 Comments: 0
Pg 1916 Pg 1917 Pg 1918 Pg 1919 Pg 1920 Pg 1921 Pg 1922 Pg 1923 Pg 1924 Pg 1925
