
AllQuestion and Answers: Page 1907
Question Number 19058 Answers: 0 Comments: 0

Question Number 19055 Answers: 1 Comments: 0
Question Number 19033 Answers: 2 Comments: 1

Question Number 19073 Answers: 0 Comments: 0
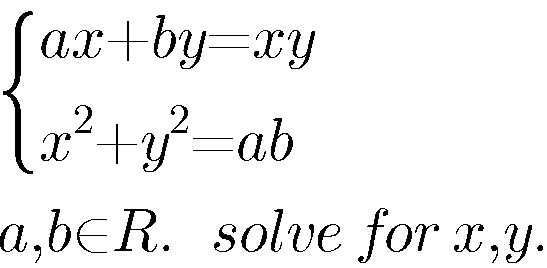
Question Number 19025 Answers: 0 Comments: 0

Question Number 19077 Answers: 1 Comments: 0
Question Number 19021 Answers: 0 Comments: 4

Question Number 19060 Answers: 1 Comments: 2

Question Number 19009 Answers: 1 Comments: 0
Question Number 19002 Answers: 1 Comments: 0
Question Number 19117 Answers: 0 Comments: 0
Question Number 19053 Answers: 1 Comments: 0
Question Number 18979 Answers: 0 Comments: 0

Question Number 18969 Answers: 1 Comments: 0
Question Number 18965 Answers: 1 Comments: 3
Question Number 18963 Answers: 0 Comments: 4
Question Number 18962 Answers: 1 Comments: 0
Question Number 18961 Answers: 1 Comments: 0
$$\mathrm{Find}\:\mathrm{arg}\left({z}\right),\:{z}\:=\:{i}^{{i}^{{i}} } . \\ $$
Question Number 18951 Answers: 0 Comments: 0

Question Number 18949 Answers: 1 Comments: 1
Question Number 18945 Answers: 0 Comments: 1
Question Number 18924 Answers: 1 Comments: 0
Question Number 18922 Answers: 0 Comments: 3
Question Number 18918 Answers: 0 Comments: 17
Question Number 18940 Answers: 0 Comments: 3
Question Number 18916 Answers: 0 Comments: 0
$${x}^{\mathrm{2}} −\mathrm{7}{x}+\mathrm{12}<{mod}\left({x}−\mathrm{4}\right) \\ $$
Pg 1902 Pg 1903 Pg 1904 Pg 1905 Pg 1906 Pg 1907 Pg 1908 Pg 1909 Pg 1910 Pg 1911
