Question and Answers Forum

AllQuestion and Answers: Page 1906

Question Number 10512 Answers: 0 Comments: 0

find C.I. and P.I. of differential equations . (d^2 y/dx^2 ) +4y=tan 2x.

$$\mathrm{find}\:\mathrm{C}.\mathrm{I}.\:\mathrm{and}\:\:\mathrm{P}.\mathrm{I}.\:\mathrm{of}\:\mathrm{differential}\:\mathrm{equations}\:. \\ $$$$\frac{\mathrm{d}^{\mathrm{2}} \mathrm{y}}{\mathrm{dx}^{\mathrm{2}} }\:+\mathrm{4y}=\mathrm{tan}\:\mathrm{2x}. \\ $$

Question Number 10510 Answers: 2 Comments: 0

Question Number 10507 Answers: 0 Comments: 0

Question Number 10528 Answers: 3 Comments: 0

Give the velocity field v = (6 + 2xy + t^2 )i − (xy^2 + 10t)j + 25k what is the acceleration of the particle at (3, 0, 2) at time t = 1.

$$\mathrm{Give}\:\mathrm{the}\:\mathrm{velocity}\:\mathrm{field} \\ $$$$\mathrm{v}\:=\:\left(\mathrm{6}\:+\:\mathrm{2xy}\:+\:\mathrm{t}^{\mathrm{2}} \right)\mathrm{i}\:−\:\left(\mathrm{xy}^{\mathrm{2}} \:+\:\mathrm{10t}\right)\mathrm{j}\:+\:\mathrm{25k} \\ $$$$\mathrm{what}\:\mathrm{is}\:\mathrm{the}\:\mathrm{acceleration}\:\mathrm{of}\:\mathrm{the}\:\mathrm{particle}\:\mathrm{at}\:\left(\mathrm{3},\:\mathrm{0},\:\mathrm{2}\right) \\ $$$$\mathrm{at}\:\mathrm{time}\:\mathrm{t}\:=\:\mathrm{1}. \\ $$

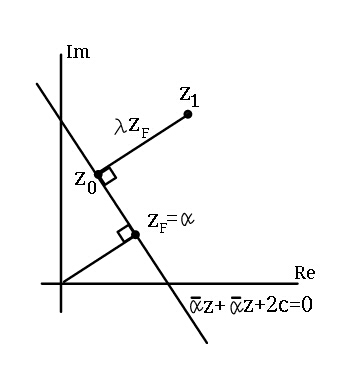
Question Number 10495 Answers: 1 Comments: 0

∫_0 ^(2π) (√(R^2 +r^2 −2Rrcos θ)) dθ

$$\int_{\mathrm{0}} ^{\mathrm{2}\pi} \sqrt{{R}^{\mathrm{2}} +{r}^{\mathrm{2}} −\mathrm{2}{Rr}\mathrm{cos}\:\theta}\:{d}\theta \\ $$

Question Number 10493 Answers: 2 Comments: 0

(1/(2!))+(2/(3!))+(3/(4!))+(4/(5!))+...+((17)/(18!))=?

$$\frac{\mathrm{1}}{\mathrm{2}!}+\frac{\mathrm{2}}{\mathrm{3}!}+\frac{\mathrm{3}}{\mathrm{4}!}+\frac{\mathrm{4}}{\mathrm{5}!}+...+\frac{\mathrm{17}}{\mathrm{18}!}=? \\ $$

Question Number 10492 Answers: 1 Comments: 0

3^(logx) −2^(logx−1) =2^(logx+1) −2×3^(logx−1) ⇒x=?

$$\mathrm{3}^{{logx}} −\mathrm{2}^{{logx}−\mathrm{1}} =\mathrm{2}^{{logx}+\mathrm{1}} −\mathrm{2}×\mathrm{3}^{{logx}−\mathrm{1}} \Rightarrow{x}=? \\ $$

Question Number 10489 Answers: 1 Comments: 0

The fifth, nineth, sixteenth terms of a linear sequence are consecutive terms of an exponential sequence . (1) Find the common difference of the linear sequence in terms of the first term (2) Show that 21^(th) , 37^(th) , 65^(th) terms of the linear sequence are consecutive terms of an exponential sequence whose common ratio is (3/4)

$$\mathrm{The}\:\mathrm{fifth},\:\mathrm{nineth},\:\mathrm{sixteenth}\:\mathrm{terms}\:\mathrm{of}\:\mathrm{a}\:\mathrm{linear}\: \\ $$$$\mathrm{sequence}\:\mathrm{are}\:\mathrm{consecutive}\:\mathrm{terms}\:\mathrm{of}\:\mathrm{an}\:\mathrm{exponential} \\ $$$$\mathrm{sequence}\:. \\ $$$$\left(\mathrm{1}\right)\:\mathrm{Find}\:\mathrm{the}\:\mathrm{common}\:\mathrm{difference}\:\mathrm{of}\:\mathrm{the}\:\mathrm{linear}\: \\ $$$$\mathrm{sequence}\:\mathrm{in}\:\mathrm{terms}\:\mathrm{of}\:\mathrm{the}\:\mathrm{first}\:\mathrm{term} \\ $$$$\left(\mathrm{2}\right)\:\mathrm{Show}\:\mathrm{that}\:\mathrm{21}^{\mathrm{th}} ,\:\mathrm{37}^{\mathrm{th}} ,\:\mathrm{65}^{\mathrm{th}} \:\mathrm{terms}\:\mathrm{of}\:\mathrm{the}\:\mathrm{linear} \\ $$$$\mathrm{sequence}\:\mathrm{are}\:\mathrm{consecutive}\:\mathrm{terms}\:\mathrm{of}\:\mathrm{an}\:\mathrm{exponential} \\ $$$$\mathrm{sequence}\:\mathrm{whose}\:\mathrm{common}\:\mathrm{ratio}\:\mathrm{is}\:\frac{\mathrm{3}}{\mathrm{4}} \\ $$

Question Number 10488 Answers: 1 Comments: 0

An exponential sequence of positive terms and a linear sequence have the same first term. the sum o their first term is 3, the sum of their second term is (3/2), and the sum of their third term is 6. find the sum of their fifth term.

$$\mathrm{An}\:\mathrm{exponential}\:\mathrm{sequence}\:\mathrm{of}\:\mathrm{positive}\:\mathrm{terms}\:\mathrm{and}\:\mathrm{a} \\ $$$$\mathrm{linear}\:\mathrm{sequence}\:\mathrm{have}\:\mathrm{the}\:\mathrm{same}\:\mathrm{first}\:\mathrm{term}.\:\mathrm{the}\:\mathrm{sum} \\ $$$$\mathrm{o}\:\mathrm{their}\:\mathrm{first}\:\mathrm{term}\:\mathrm{is}\:\mathrm{3},\:\mathrm{the}\:\mathrm{sum}\:\mathrm{of}\:\mathrm{their}\:\mathrm{second}\:\mathrm{term} \\ $$$$\mathrm{is}\:\frac{\mathrm{3}}{\mathrm{2}},\:\mathrm{and}\:\mathrm{the}\:\mathrm{sum}\:\mathrm{of}\:\mathrm{their}\:\mathrm{third}\:\mathrm{term}\:\mathrm{is}\:\mathrm{6}.\:\mathrm{find}\:\mathrm{the} \\ $$$$\mathrm{sum}\:\mathrm{of}\:\mathrm{their}\:\mathrm{fifth}\:\mathrm{term}. \\ $$

Question Number 10487 Answers: 1 Comments: 0

A sequence of numbers T_1 ,T_2 ,T_3 ,....... T_(n ) satisfies the relation T_(n + 1) + n^2 = nT_n + 2 for all integers n≥1. if T_1 = 2. find (a) The values of T_2 , T_3 , T_4 (b) An expression for T_n in terms of the sequence (c) The sum of the first nth terms of the sequence (d) The sum of T_n + T_(n + 1) + T_(n + 2) when n = 20

$$\mathrm{A}\:\mathrm{sequence}\:\mathrm{of}\:\mathrm{numbers}\:\mathrm{T}_{\mathrm{1}} ,\mathrm{T}_{\mathrm{2}} ,\mathrm{T}_{\mathrm{3}} ,.......\:\mathrm{T}_{\mathrm{n}\:} \mathrm{satisfies} \\ $$$$\mathrm{the}\:\mathrm{relation}\:\mathrm{T}_{\mathrm{n}\:+\:\mathrm{1}} \:+\:\mathrm{n}^{\mathrm{2}} \:=\:\mathrm{nT}_{\mathrm{n}} \:+\:\mathrm{2}\:\mathrm{for}\:\mathrm{all}\:\mathrm{integers} \\ $$$$\mathrm{n}\geqslant\mathrm{1}.\:\mathrm{if}\:\mathrm{T}_{\mathrm{1}} \:=\:\mathrm{2}.\:\mathrm{find}\: \\ $$$$\left(\mathrm{a}\right)\:\mathrm{The}\:\mathrm{values}\:\mathrm{of}\:\mathrm{T}_{\mathrm{2}} ,\:\mathrm{T}_{\mathrm{3}} ,\:\mathrm{T}_{\mathrm{4}} \\ $$$$\left(\mathrm{b}\right)\:\mathrm{An}\:\mathrm{expression}\:\mathrm{for}\:\mathrm{T}_{\mathrm{n}} \:\mathrm{in}\:\mathrm{terms}\:\mathrm{of}\:\mathrm{the}\:\mathrm{sequence} \\ $$$$\left(\mathrm{c}\right)\:\mathrm{The}\:\mathrm{sum}\:\mathrm{of}\:\mathrm{the}\:\mathrm{first}\:\mathrm{nth}\:\mathrm{terms}\:\mathrm{of}\:\mathrm{the}\:\mathrm{sequence} \\ $$$$\left(\mathrm{d}\right)\:\mathrm{The}\:\mathrm{sum}\:\mathrm{of}\:\mathrm{T}_{\mathrm{n}} \:+\:\mathrm{T}_{\mathrm{n}\:+\:\mathrm{1}} \:+\:\mathrm{T}_{\mathrm{n}\:+\:\mathrm{2}} \:\:\mathrm{when}\:\mathrm{n}\:=\:\mathrm{20} \\ $$

Question Number 10485 Answers: 1 Comments: 0

A sequence of numbers T_1 , T_2 , T_3 , ... Satisfies the relation 3T_n = T_(n − 1) + 6, Show that for all values of n ≥ 1, T_n − 3 = (1/3)(T_(n − 3) − 3). Hence or otherwise show that if T_1 = 4, T_n = 3 + 3^(1 − n) for all values of n, also find the sum of the first five terms of the sequence.

$$\mathrm{A}\:\mathrm{sequence}\:\mathrm{of}\:\mathrm{numbers}\:\mathrm{T}_{\mathrm{1}} ,\:\mathrm{T}_{\mathrm{2}} ,\:\mathrm{T}_{\mathrm{3}} ,\:...\:\:\mathrm{Satisfies}\:\mathrm{the} \\ $$$$\mathrm{relation}\:\mathrm{3T}_{\mathrm{n}} =\:\mathrm{T}_{\mathrm{n}\:−\:\mathrm{1}} \:+\:\mathrm{6},\:\mathrm{Show}\:\mathrm{that}\:\mathrm{for}\:\mathrm{all}\:\mathrm{values}\: \\ $$$$\mathrm{of}\:\mathrm{n}\:\geqslant\:\mathrm{1},\:\mathrm{T}_{\mathrm{n}} −\:\mathrm{3}\:\:=\:\frac{\mathrm{1}}{\mathrm{3}}\left(\mathrm{T}_{\mathrm{n}\:−\:\mathrm{3}} \:−\:\mathrm{3}\right).\:\mathrm{Hence}\:\mathrm{or}\:\mathrm{otherwise} \\ $$$$\mathrm{show}\:\mathrm{that}\:\mathrm{if}\:\mathrm{T}_{\mathrm{1}} \:=\:\mathrm{4},\:\mathrm{T}_{\mathrm{n}} \:=\:\mathrm{3}\:+\:\mathrm{3}^{\mathrm{1}\:−\:\mathrm{n}} \:\:\mathrm{for}\:\mathrm{all}\:\mathrm{values}\:\mathrm{of} \\ $$$$\mathrm{n},\:\mathrm{also}\:\mathrm{find}\:\mathrm{the}\:\mathrm{sum}\:\mathrm{of}\:\mathrm{the}\:\mathrm{first}\:\mathrm{five}\:\mathrm{terms}\:\mathrm{of}\:\mathrm{the}\: \\ $$$$\mathrm{sequence}. \\ $$

Question Number 10483 Answers: 0 Comments: 0

Question Number 10480 Answers: 2 Comments: 0

d/dx(cos^2 xdy/dx)=0

$${d}/{dx}\left(\mathrm{cos}\:^{\mathrm{2}} {xdy}/{dx}\right)=\mathrm{0} \\ $$$$ \\ $$

Question Number 10477 Answers: 0 Comments: 0

maximum and minimum value of 12x^(5−5x^4_(+40x^3_(+6) ) )

$${maximum}\:{and}\:{minimum}\:{value}\:{of}\: \\ $$$$\mathrm{12}{x}^{\mathrm{5}−\mathrm{5}{x}^{\mathrm{4}_{+\mathrm{40}{x}^{\mathrm{3}_{+\mathrm{6}} } } } } \\ $$

Question Number 10475 Answers: 1 Comments: 0

aman walks 600m at a bearing of 45^(0 ) then 500m at a bearing 90^0 then 300m at bearing of 135^(0 ) then 400m at a bearing of 225^0 .find the resultant displacement which the man has made

$${aman}\:{walks}\:\mathrm{600}{m}\:{at}\:{a}\:{bearing}\:{of}\: \\ $$$$\mathrm{45}^{\mathrm{0}\:} {then}\:\mathrm{500}{m}\:{at}\:{a}\:{bearing}\:\mathrm{90}^{\mathrm{0}} \: \\ $$$${then}\:\mathrm{300}{m}\:{at}\:{bearing}\:{of}\:\mathrm{135}^{\mathrm{0}\:} \: \\ $$$${then}\:\mathrm{400}{m}\:{at}\:{a}\:{bearing}\:{of}\:\mathrm{225}^{\mathrm{0}} \\ $$$$.{find}\:{the}\:{resultant}\:{displacement} \\ $$$${which}\:{the}\:{man}\:{has}\:{made} \\ $$

Question Number 10474 Answers: 0 Comments: 1

Just so you all know, I had to make a new username. I am FilupSmith

$$\mathrm{Just}\:\mathrm{so}\:\mathrm{you}\:\mathrm{all}\:\mathrm{know},\:\mathrm{I}\:\mathrm{had}\:\mathrm{to}\:\mathrm{make} \\ $$$$\mathrm{a}\:\mathrm{new}\:\mathrm{username}.\:\mathrm{I}\:\mathrm{am}\:\mathrm{FilupSmith} \\ $$

Question Number 10472 Answers: 0 Comments: 1

My name is Wilton Stewart i have problem with math i would like some help.

$${My}\:{name}\:{is}\:{Wilton}\:{Stewart}\:{i}\:{have}\:{problem}\:{with}\:{math}\:{i}\:{would}\:{like}\:{some}\:{help}. \\ $$$$ \\ $$

Question Number 10470 Answers: 1 Comments: 0

Question Number 10469 Answers: 0 Comments: 0

One definition of Γ(x+1) is: Γ(x+1)=∫_0 ^( ∞) e^(−t) t^x dx According to WolframAlpha, another definition is: Γ(x+1)=(1/(e^(2iπx) −1))∮_L e^(−t) t^x dx Can someone explian to me where this comes from and what it means. Also, its been a long time since I learnt contour integrals, so what does ∮_L mean?

$$\mathrm{One}\:\mathrm{definition}\:\mathrm{of}\:\:\Gamma\left({x}+\mathrm{1}\right)\:\:\mathrm{is}: \\ $$$$\Gamma\left({x}+\mathrm{1}\right)=\int_{\mathrm{0}} ^{\:\infty} {e}^{−{t}} {t}^{{x}} {dx} \\ $$$$\: \\ $$$$\mathrm{According}\:\mathrm{to}\:\mathrm{WolframAlpha},\:\mathrm{another} \\ $$$$\mathrm{definition}\:\mathrm{is}: \\ $$$$\Gamma\left({x}+\mathrm{1}\right)=\frac{\mathrm{1}}{{e}^{\mathrm{2}{i}\pi{x}} −\mathrm{1}}\oint_{{L}} {e}^{−{t}} {t}^{{x}} {dx} \\ $$$$\mathrm{Can}\:\mathrm{someone}\:\mathrm{explian}\:\mathrm{to}\:\mathrm{me}\:\mathrm{where}\:\mathrm{this} \\ $$$$\mathrm{comes}\:\mathrm{from}\:\mathrm{and}\:\mathrm{what}\:\mathrm{it}\:\mathrm{means}. \\ $$$$\: \\ $$$$\mathrm{Also},\:\mathrm{its}\:\mathrm{been}\:\mathrm{a}\:\mathrm{long}\:\mathrm{time}\:\mathrm{since}\:\mathrm{I}\:\mathrm{learnt} \\ $$$$\mathrm{contour}\:\mathrm{integrals},\:\mathrm{so}\:\mathrm{what}\:\mathrm{does}\:\oint_{{L}} \:\mathrm{mean}? \\ $$

Question Number 10468 Answers: 0 Comments: 0

Show why: Γ(x+1)≈(√(2π))e^(−x) x^(x+(1/2))

$$\mathrm{Show}\:\mathrm{why}: \\ $$$$\Gamma\left({x}+\mathrm{1}\right)\approx\sqrt{\mathrm{2}\pi}{e}^{−{x}} {x}^{{x}+\frac{\mathrm{1}}{\mathrm{2}}} \\ $$

Question Number 10464 Answers: 1 Comments: 0