
AllQuestion and Answers: Page 1904
Question Number 19884 Answers: 1 Comments: 1

Question Number 19877 Answers: 0 Comments: 0

Question Number 19875 Answers: 1 Comments: 1
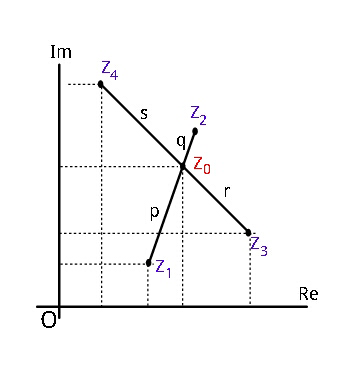
Question Number 19860 Answers: 1 Comments: 0
Question Number 19859 Answers: 0 Comments: 1
Question Number 19857 Answers: 0 Comments: 3
Question Number 19822 Answers: 1 Comments: 0
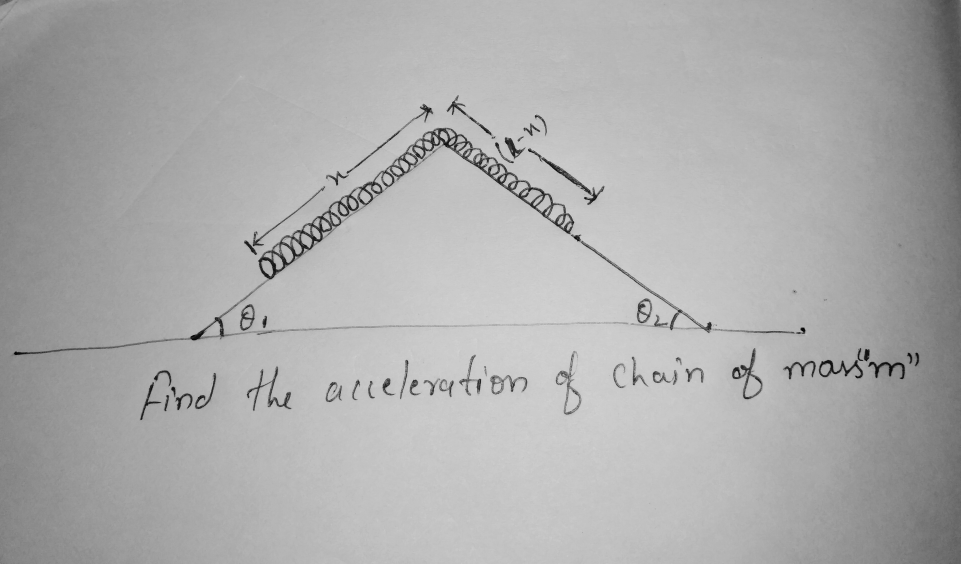
Question Number 19812 Answers: 1 Comments: 0
Question Number 19811 Answers: 0 Comments: 2
Question Number 19809 Answers: 1 Comments: 0
Question Number 19978 Answers: 1 Comments: 0
Question Number 19799 Answers: 0 Comments: 2
Question Number 19796 Answers: 1 Comments: 1
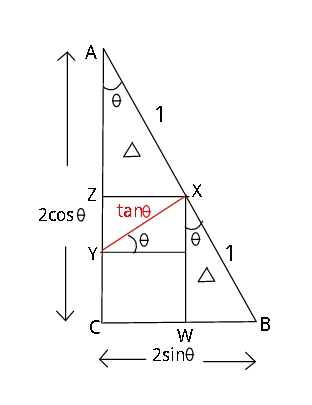
Question Number 19795 Answers: 1 Comments: 0
Question Number 19794 Answers: 0 Comments: 0
Question Number 19792 Answers: 2 Comments: 0
Question Number 19828 Answers: 1 Comments: 1
Question Number 19774 Answers: 1 Comments: 0
Question Number 19760 Answers: 1 Comments: 0
Question Number 19758 Answers: 1 Comments: 1
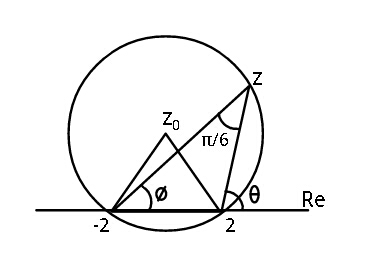
Question Number 19741 Answers: 0 Comments: 1
Question Number 19740 Answers: 1 Comments: 0
Question Number 19739 Answers: 1 Comments: 0
Question Number 19738 Answers: 1 Comments: 1
Question Number 19736 Answers: 1 Comments: 1

Question Number 19735 Answers: 1 Comments: 0
Pg 1899 Pg 1900 Pg 1901 Pg 1902 Pg 1903 Pg 1904 Pg 1905 Pg 1906 Pg 1907 Pg 1908
