Question and Answers Forum

AllQuestion and Answers: Page 190

Question Number 203396 Answers: 0 Comments: 0

State the completness axioms of the real number

$$\mathrm{State}\:\mathrm{the}\:\mathrm{completness}\:\mathrm{axioms}\:\mathrm{of}\:\mathrm{the} \\ $$$$\mathrm{real}\:\mathrm{number} \\ $$

Question Number 203394 Answers: 1 Comments: 0

Question Number 203393 Answers: 0 Comments: 0

Question Number 203392 Answers: 0 Comments: 2

Question Number 203389 Answers: 1 Comments: 0

Question Number 203387 Answers: 1 Comments: 0

Question Number 203379 Answers: 0 Comments: 0

If a,b,c ∈R^+ with a+b+c=3 prove that (1/(a^6 +b^6 +3c^3 +4))+(1/(b^6 +c^6 +3a^3 +4))+(1/(c^6 +a^6 +3b^3 +4))≤(3/(3+2((√(ab))+(√(bc))+(√(ac)))))

$$\mathrm{If}\:{a},{b},{c}\:\in\mathbb{R}^{+} \:\mathrm{with}\:{a}+{b}+{c}=\mathrm{3}\:\mathrm{prove}\:\mathrm{that} \\ $$$$\frac{\mathrm{1}}{{a}^{\mathrm{6}} +{b}^{\mathrm{6}} +\mathrm{3}{c}^{\mathrm{3}} +\mathrm{4}}+\frac{\mathrm{1}}{{b}^{\mathrm{6}} +{c}^{\mathrm{6}} +\mathrm{3}{a}^{\mathrm{3}} +\mathrm{4}}+\frac{\mathrm{1}}{{c}^{\mathrm{6}} +{a}^{\mathrm{6}} +\mathrm{3}{b}^{\mathrm{3}} +\mathrm{4}}\leqslant\frac{\mathrm{3}}{\mathrm{3}+\mathrm{2}\left(\sqrt{{ab}}+\sqrt{{bc}}+\sqrt{{ac}}\right)} \\ $$

Question Number 203378 Answers: 0 Comments: 0

Question Number 203385 Answers: 2 Comments: 0

Question Number 203401 Answers: 2 Comments: 0

Question Number 203375 Answers: 0 Comments: 4

valeur x? (∡ECA =90)

$$\:\mathrm{valeur}\:\boldsymbol{\mathrm{x}}? \\ $$$$\left(\measuredangle\mathrm{ECA}\:\:=\mathrm{90}\right) \\ $$

Question Number 203374 Answers: 3 Comments: 0

Question Number 203370 Answers: 1 Comments: 1

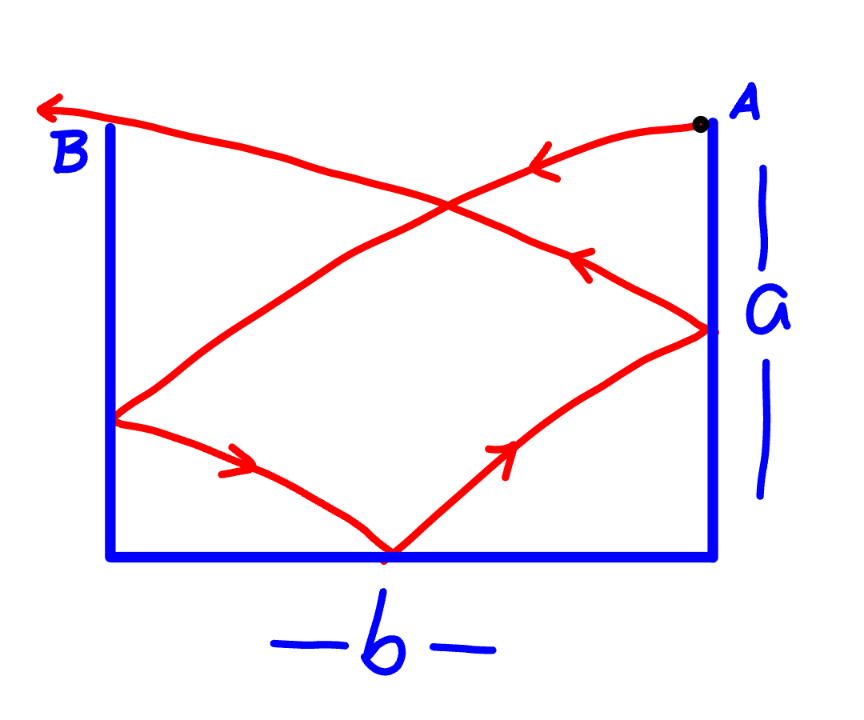
Question Number 203367 Answers: 2 Comments: 0

if a+b=198, what is the largest integer root which the equation x^2 +ax+b=0 may have?

$${if}\:\boldsymbol{{a}}+\boldsymbol{{b}}=\mathrm{198},\:{what}\:{is}\:{the}\:{largest} \\ $$$$\boldsymbol{{integer}}\:{root}\:{which}\:{the}\:{equation} \\ $$$$\boldsymbol{{x}}^{\mathrm{2}} +\boldsymbol{{ax}}+\boldsymbol{{b}}=\mathrm{0}\:{may}\:{have}? \\ $$

Question Number 203357 Answers: 1 Comments: 0

For the series 5−(5/2)+(5/4)−(5/8)+∙∙∙+(((−1)^(n−1) 5)/2^(n−1) ) find an expression for the sum of the first n terms. Also if the series converges, find the sum to ∞.

$$\boldsymbol{{For}}\:\boldsymbol{{the}}\:\boldsymbol{{series}}\:\mathrm{5}−\frac{\mathrm{5}}{\mathrm{2}}+\frac{\mathrm{5}}{\mathrm{4}}−\frac{\mathrm{5}}{\mathrm{8}}+\centerdot\centerdot\centerdot+\frac{\left(−\mathrm{1}\right)^{\boldsymbol{{n}}−\mathrm{1}} \mathrm{5}}{\mathrm{2}^{\boldsymbol{{n}}−\mathrm{1}} } \\ $$$$\boldsymbol{{find}}\:\boldsymbol{{an}}\:\boldsymbol{{expression}}\:\boldsymbol{{for}}\:\boldsymbol{{the}}\:\boldsymbol{{sum}}\:\boldsymbol{{of}}\:\boldsymbol{{the}}\:\boldsymbol{{first}} \\ $$$$\boldsymbol{{n}}\:\boldsymbol{{terms}}.\:\boldsymbol{{Also}}\:\boldsymbol{{if}}\:\boldsymbol{{the}}\:\boldsymbol{{series}}\:\boldsymbol{{converges}}, \\ $$$$\boldsymbol{{find}}\:\boldsymbol{{the}}\:\boldsymbol{{sum}}\:\boldsymbol{{to}}\:\infty. \\ $$$$ \\ $$$$ \\ $$

Question Number 203354 Answers: 1 Comments: 0

$$. \\ $$

Question Number 203353 Answers: 0 Comments: 0

Question Number 203352 Answers: 1 Comments: 0

Question Number 203351 Answers: 1 Comments: 0

Question Number 203349 Answers: 1 Comments: 0

calculate ∫∫_([0,a]^2 ) e^(−x^2 −y^2 ) dxdy can you find ∫_0 ^a e^(−x^2 ) dx ? a>0

$${calculate}\:\int\int_{\left[\mathrm{0},{a}\right]^{\mathrm{2}} } \:{e}^{−{x}^{\mathrm{2}} −{y}^{\mathrm{2}} } {dxdy} \\ $$$${can}\:{you}\:{find}\:\int_{\mathrm{0}} ^{{a}} {e}^{−{x}^{\mathrm{2}} } {dx}\:\:\:\:? \\ $$$${a}>\mathrm{0} \\ $$

Question Number 203336 Answers: 0 Comments: 0

Question Number 203330 Answers: 2 Comments: 0

Question Number 203329 Answers: 1 Comments: 0

find the ranges of value of x for which series convergent or divergent 𝚺_(n=1) ^∞ (((n+1))/n^3 )x^n

$$\boldsymbol{{find}}\:\boldsymbol{{the}}\:\boldsymbol{{ranges}}\:\boldsymbol{{of}}\:\boldsymbol{{value}}\:\boldsymbol{{of}}\:\boldsymbol{{x}}\:\boldsymbol{{for}}\:\boldsymbol{{which}}\: \\ $$$$\boldsymbol{{series}}\:\boldsymbol{{convergent}}\:\boldsymbol{{or}}\:\boldsymbol{{divergent}} \\ $$$$\underset{\boldsymbol{{n}}=\mathrm{1}} {\overset{\infty} {\boldsymbol{\sum}}}\frac{\left(\boldsymbol{{n}}+\mathrm{1}\right)}{\boldsymbol{{n}}^{\mathrm{3}} }\boldsymbol{{x}}^{\boldsymbol{{n}}} \\ $$

Question Number 203327 Answers: 2 Comments: 0

Question Number 203325 Answers: 1 Comments: 0

sin^2 x+cos^2 (2x)+sin^2 (3x)=(3/2)

$$\mathrm{sin}^{\mathrm{2}} {x}+\mathrm{cos}^{\mathrm{2}} \left(\mathrm{2}{x}\right)+\mathrm{sin}^{\mathrm{2}} \left(\mathrm{3}{x}\right)=\frac{\mathrm{3}}{\mathrm{2}} \\ $$

Question Number 203321 Answers: 1 Comments: 0

Help-me! Observe points A, B and C below and find the widthof a lake according to the following data: (AB)m; C^ = 39°52′12′′ (BC − 257.5)m; A^ = 97°7′56′′ (CA − 30)m; B^ = 42°59′52′′ CA is the width of the lake •^C •_A •_B

$$\mathrm{Help}-\mathrm{me}! \\ $$$$\: \\ $$$$\mathrm{Observe}\:\mathrm{points}\:\mathrm{A},\:\mathrm{B}\:\mathrm{and}\:\mathrm{C}\:\mathrm{below}\:\mathrm{and}\:\mathrm{find}\:\mathrm{the}\:\mathrm{widthof}\:\mathrm{a}\:\mathrm{lake}\:\mathrm{according}\:\mathrm{to}\:\mathrm{the}\:\mathrm{following}\:\mathrm{data}: \\ $$$$\: \\ $$$$\left(\mathrm{AB}\right)\mathrm{m};\:\hat {\mathrm{C}}\:=\:\mathrm{39}°\mathrm{52}'\mathrm{12}'' \\ $$$$\left(\mathrm{BC}\:−\:\mathrm{257}.\mathrm{5}\right)\mathrm{m};\:\hat {\mathrm{A}}\:=\:\mathrm{97}°\mathrm{7}'\mathrm{56}'' \\ $$$$\left(\mathrm{CA}\:−\:\mathrm{30}\right)\mathrm{m};\:\hat {\mathrm{B}}\:=\:\mathrm{42}°\mathrm{59}'\mathrm{52}'' \\ $$$$\mathrm{CA}\:\mathrm{is}\:\mathrm{the}\:\mathrm{width}\:\mathrm{of}\:\mathrm{the}\:\mathrm{lake}\: \\ $$$$\: \\ $$$$\bullet^{\mathrm{C}} \\ $$$$\: \\ $$$$\: \\ $$$$\: \\ $$$$\: \\ $$$$\: \\ $$$$\: \\ $$$$\bullet_{\mathrm{A}} \\ $$$$\: \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\bullet_{\mathrm{B}} \\ $$

Pg 185 Pg 186 Pg 187 Pg 188 Pg 189 Pg 190 Pg 191 Pg 192 Pg 193 Pg 194

Contact: info@tinkutara.com