
AllQuestion and Answers: Page 1898
Question Number 20149 Answers: 2 Comments: 1

Question Number 20162 Answers: 1 Comments: 0
Question Number 20138 Answers: 1 Comments: 0
Question Number 20118 Answers: 1 Comments: 0
Question Number 20116 Answers: 1 Comments: 0
Question Number 20115 Answers: 1 Comments: 0
Question Number 20110 Answers: 0 Comments: 1

Question Number 20102 Answers: 2 Comments: 0
Question Number 20091 Answers: 1 Comments: 0
Question Number 20079 Answers: 0 Comments: 2

Question Number 20068 Answers: 1 Comments: 1

Question Number 20058 Answers: 1 Comments: 0
Question Number 20054 Answers: 1 Comments: 0
Question Number 20053 Answers: 1 Comments: 0
Question Number 20052 Answers: 1 Comments: 0
Question Number 20049 Answers: 0 Comments: 0
Question Number 20047 Answers: 1 Comments: 0
Question Number 20042 Answers: 0 Comments: 3
Question Number 20040 Answers: 0 Comments: 3
Question Number 20038 Answers: 1 Comments: 1
Question Number 20036 Answers: 1 Comments: 0
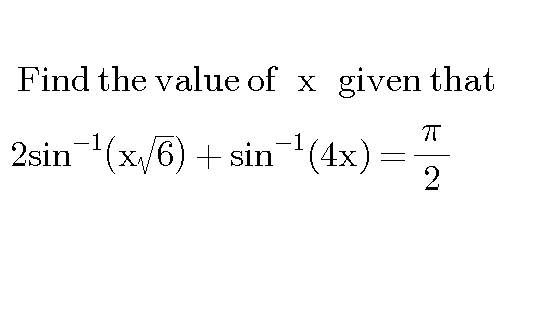
Question Number 20031 Answers: 1 Comments: 0
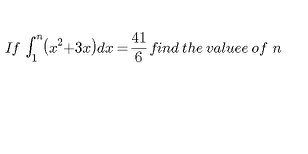
Question Number 20035 Answers: 1 Comments: 1
Question Number 20051 Answers: 1 Comments: 0
Question Number 20021 Answers: 1 Comments: 0
Question Number 20019 Answers: 1 Comments: 0
Pg 1893 Pg 1894 Pg 1895 Pg 1896 Pg 1897 Pg 1898 Pg 1899 Pg 1900 Pg 1901 Pg 1902
