Question and Answers Forum

AllQuestion and Answers: Page 1896

Question Number 20652 Answers: 0 Comments: 4

Suppose x is a positive real number such that {x}, [x] and x are in a geometric progression. Find the least positive integer n such that x^n > 100. (Here [x] denotes the integer part of x and {x} = x − [x].)

$$\mathrm{Suppose}\:{x}\:\mathrm{is}\:\mathrm{a}\:\mathrm{positive}\:\mathrm{real}\:\mathrm{number} \\ $$$$\mathrm{such}\:\mathrm{that}\:\left\{{x}\right\},\:\left[{x}\right]\:\mathrm{and}\:{x}\:\mathrm{are}\:\mathrm{in}\:\mathrm{a} \\ $$$$\mathrm{geometric}\:\mathrm{progression}.\:\mathrm{Find}\:\mathrm{the}\:\mathrm{least} \\ $$$$\mathrm{positive}\:\mathrm{integer}\:{n}\:\mathrm{such}\:\mathrm{that}\:{x}^{{n}} \:>\:\mathrm{100}. \\ $$$$\left(\mathrm{Here}\:\left[{x}\right]\:\mathrm{denotes}\:\mathrm{the}\:\mathrm{integer}\:\mathrm{part}\:\mathrm{of}\:{x}\right. \\ $$$$\left.\mathrm{and}\:\left\{{x}\right\}\:=\:{x}\:−\:\left[{x}\right].\right) \\ $$

Question Number 20648 Answers: 1 Comments: 0

If (F/(sin (A − a))) = (W/(sin A)), prove that tan A = ((W sin a)/(W cos a − F))

$$\mathrm{If}\:\:\frac{{F}}{\mathrm{sin}\:\left({A}\:−\:{a}\right)}\:=\:\frac{{W}}{\mathrm{sin}\:{A}},\:\:\mathrm{prove}\:\mathrm{that} \\ $$$$\mathrm{tan}\:{A}\:=\:\frac{{W}\:\mathrm{sin}\:{a}}{{W}\:\mathrm{cos}\:{a}\:−\:{F}} \\ $$

Question Number 20647 Answers: 1 Comments: 0

prove it, tan (α+(π/3))+tan (α−(π/3))=((4sin 2α)/(1−4sin^2 α))

$${prove}\:{it}, \\ $$$$\mathrm{tan}\:\left(\alpha+\frac{\pi}{\mathrm{3}}\right)+\mathrm{tan}\:\left(\alpha−\frac{\pi}{\mathrm{3}}\right)=\frac{\mathrm{4sin}\:\mathrm{2}\alpha}{\mathrm{1}−\mathrm{4sin}\:^{\mathrm{2}} \alpha} \\ $$

Question Number 20646 Answers: 1 Comments: 0

if cos (β−γ)+cos( γ−α)+cos (α−β)=−(3/2) so proof it, Σcos α=0,Σsin α=0

$${if}\:\mathrm{cos}\:\left(\beta−\gamma\right)+\mathrm{cos}\left(\:\gamma−\alpha\right)+\mathrm{cos}\:\left(\alpha−\beta\right)=−\frac{\mathrm{3}}{\mathrm{2}} \\ $$$${so}\:{proof}\:{it}, \\ $$$$\Sigma\mathrm{cos}\:\alpha=\mathrm{0},\Sigma\mathrm{sin}\:\alpha=\mathrm{0} \\ $$

Question Number 20664 Answers: 0 Comments: 0

In what time shall a carpet of length l and radius R unroll on a flat rough ground if given a little push to start the motion.

$${In}\:{what}\:{time}\:{shall}\:{a}\:{carpet}\:{of} \\ $$$${length}\:\boldsymbol{{l}}\:{and}\:{radius}\:\boldsymbol{{R}}\:{unroll}\:{on} \\ $$$${a}\:{flat}\:{rough}\:{ground}\:{if}\:{given}\:{a}\: \\ $$$${little}\:{push}\:{to}\:{start}\:{the}\:{motion}. \\ $$

Question Number 20639 Answers: 2 Comments: 0

if cos (A+B)sin (C+D)=cos (A−B) sin (C−D) so proof cot Acot Bcot C=cot D

$${if}\:\mathrm{cos}\:\left({A}+{B}\right)\mathrm{sin}\:\left({C}+{D}\right)=\mathrm{cos}\:\left({A}−{B}\right) \\ $$$$\mathrm{sin}\:\left({C}−{D}\right) \\ $$$${so}\:{proof}\:\mathrm{cot}\:{A}\mathrm{cot}\:{B}\mathrm{cot}\:{C}=\mathrm{cot}\:{D} \\ $$

Question Number 20640 Answers: 1 Comments: 0

sin θ=Kcos (θ−α) so proof it,cot θ=((1−Ksin α)/(Kcos α))

$$\mathrm{sin}\:\theta={K}\mathrm{cos}\:\left(\theta−\alpha\right) \\ $$$${so}\:{proof}\:{it},\mathrm{cot}\:\theta=\frac{\mathrm{1}−{K}\mathrm{sin}\:\alpha}{{K}\mathrm{cos}\:\alpha} \\ $$

Question Number 20626 Answers: 1 Comments: 0

Question Number 20625 Answers: 1 Comments: 1

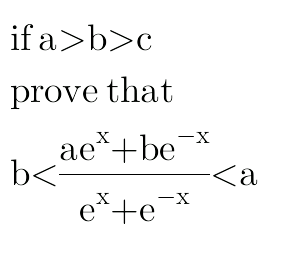
Question Number 20726 Answers: 1 Comments: 0

Five distinct 2-digit numbers are in a geometric progression. Find the middle term.

$$\mathrm{Five}\:\mathrm{distinct}\:\mathrm{2}-\mathrm{digit}\:\mathrm{numbers}\:\mathrm{are}\:\mathrm{in}\:\mathrm{a} \\ $$$$\mathrm{geometric}\:\mathrm{progression}.\:\mathrm{Find}\:\mathrm{the}\:\mathrm{middle} \\ $$$$\mathrm{term}. \\ $$

Question Number 20612 Answers: 1 Comments: 0

Evaluate ∫_0 ^( ∞) ∫_0 ^( ∞) e^(−(x^2 +y^2 )) dydx .

$${Evaluate}\:\int_{\mathrm{0}} ^{\:\:\infty} \int_{\mathrm{0}} ^{\:\:\infty} {e}^{−\left({x}^{\mathrm{2}} +{y}^{\mathrm{2}} \right)} {dydx}\:. \\ $$

Question Number 20599 Answers: 1 Comments: 0

In a rectangle ABCD, E is the midpoint of AB; F is a point on AC such that BF is perpendicular to AC; and FE perpendicular to BD. Suppose BC = 8(√3). Find AB.

$$\mathrm{In}\:\mathrm{a}\:\mathrm{rectangle}\:{ABCD},\:{E}\:\mathrm{is}\:\mathrm{the}\:\mathrm{midpoint} \\ $$$$\mathrm{of}\:{AB};\:{F}\:\mathrm{is}\:\mathrm{a}\:\mathrm{point}\:\mathrm{on}\:{AC}\:\mathrm{such}\:\mathrm{that}\:{BF} \\ $$$$\mathrm{is}\:\mathrm{perpendicular}\:\mathrm{to}\:{AC};\:\mathrm{and}\:{FE} \\ $$$$\mathrm{perpendicular}\:\mathrm{to}\:{BD}.\:\mathrm{Suppose}\:{BC}\:=\:\mathrm{8}\sqrt{\mathrm{3}}. \\ $$$$\mathrm{Find}\:{AB}. \\ $$

Question Number 20619 Answers: 1 Comments: 0

Solve the equation z^(n−1) = z^ (n ∈ N)

$${Solve}\:{the}\:{equation}\:{z}^{{n}−\mathrm{1}} \:=\:\bar {{z}}\:\left({n}\:\in\:{N}\right) \\ $$

Question Number 20631 Answers: 2 Comments: 0

Solve the inequality (x + 3)^5 − (x − 1)^5 ≥ 244.

$${Solve}\:{the}\:{inequality} \\ $$$$\left({x}\:+\:\mathrm{3}\right)^{\mathrm{5}} \:−\:\left({x}\:−\:\mathrm{1}\right)^{\mathrm{5}} \:\geqslant\:\mathrm{244}. \\ $$

Question Number 20616 Answers: 0 Comments: 1

x=rcos θcos ∅,y=rsin θsin ∅,z=sin θ then prove that x^2 +y^2 +z^2 =r^2

$${x}={r}\mathrm{cos}\:\theta\mathrm{cos}\:\emptyset,{y}={r}\mathrm{sin}\:\theta\mathrm{sin}\:\emptyset,{z}=\mathrm{sin}\:\theta \\ $$$${then}\:{prove}\:{that}\:{x}^{\mathrm{2}} +{y}^{\mathrm{2}} +{z}^{\mathrm{2}} ={r}^{\mathrm{2}} \\ $$

Question Number 20613 Answers: 0 Comments: 2

Question Number 20581 Answers: 0 Comments: 5

The surface between wedge and block is rough (Coefficient of friction μ). Find out the range of F such that, there is no relative motion between wedge and block. The wedge can move freely on smooth ground.

$${The}\:{surface}\:{between}\:{wedge}\:{and}\:{block} \\ $$$${is}\:{rough}\:\left({Coefficient}\:{of}\:{friction}\:\mu\right). \\ $$$${Find}\:{out}\:{the}\:{range}\:{of}\:{F}\:{such}\:{that}, \\ $$$${there}\:{is}\:{no}\:{relative}\:{motion}\:{between} \\ $$$${wedge}\:{and}\:{block}.\:{The}\:{wedge}\:{can}\:{move} \\ $$$${freely}\:{on}\:{smooth}\:{ground}. \\ $$

Question Number 20579 Answers: 0 Comments: 3

A 1 kg block is being pushed against a wall by a force F = 75 N as shown in the figure. The coefficient of friction is 0.25. The magnitude of acceleration of the block is

$$\mathrm{A}\:\mathrm{1}\:\mathrm{kg}\:\mathrm{block}\:\mathrm{is}\:\mathrm{being}\:\mathrm{pushed}\:\mathrm{against}\:\mathrm{a} \\ $$$$\mathrm{wall}\:\mathrm{by}\:\mathrm{a}\:\mathrm{force}\:{F}\:=\:\mathrm{75}\:\mathrm{N}\:\mathrm{as}\:\mathrm{shown}\:\mathrm{in} \\ $$$$\mathrm{the}\:\mathrm{figure}.\:\mathrm{The}\:\mathrm{coefficient}\:\mathrm{of}\:\mathrm{friction}\:\mathrm{is} \\ $$$$\mathrm{0}.\mathrm{25}.\:\mathrm{The}\:\mathrm{magnitude}\:\mathrm{of}\:\mathrm{acceleration}\:\mathrm{of} \\ $$$$\mathrm{the}\:\mathrm{block}\:\mathrm{is} \\ $$

Question Number 20561 Answers: 1 Comments: 0