Question and Answers Forum

AllQuestion and Answers: Page 1890

Question Number 18924 Answers: 1 Comments: 0

A spring of force constant k is cut into two pieces such that one piece is twice as long as the other. Then the longer piece will have a force constant of

$$\mathrm{A}\:\mathrm{spring}\:\mathrm{of}\:\mathrm{force}\:\mathrm{constant}\:{k}\:\mathrm{is}\:\mathrm{cut}\:\mathrm{into} \\ $$$$\mathrm{two}\:\mathrm{pieces}\:\mathrm{such}\:\mathrm{that}\:\mathrm{one}\:\mathrm{piece}\:\mathrm{is}\:\mathrm{twice} \\ $$$$\mathrm{as}\:\mathrm{long}\:\mathrm{as}\:\mathrm{the}\:\mathrm{other}.\:\mathrm{Then}\:\mathrm{the}\:\mathrm{longer} \\ $$$$\mathrm{piece}\:\mathrm{will}\:\mathrm{have}\:\mathrm{a}\:\mathrm{force}\:\mathrm{constant}\:\mathrm{of} \\ $$

Question Number 18922 Answers: 0 Comments: 3

Consider a block sliding over a smooth inclined surface of inclination θ. Relating to Newton′s second law applied on the block, select the incorrect alternative. (1) ΣF_(y′) ≠ 0 (2) ΣF_y = 0 (3) ΣF_x = −mg sin θ (4) ΣF_(x′) < 0

$$\mathrm{Consider}\:\mathrm{a}\:\mathrm{block}\:\mathrm{sliding}\:\mathrm{over}\:\mathrm{a}\:\mathrm{smooth} \\ $$$$\mathrm{inclined}\:\mathrm{surface}\:\mathrm{of}\:\mathrm{inclination}\:\theta.\:\mathrm{Relating} \\ $$$$\mathrm{to}\:\mathrm{Newton}'\mathrm{s}\:\mathrm{second}\:\mathrm{law}\:\mathrm{applied}\:\mathrm{on}\:\mathrm{the} \\ $$$$\mathrm{block},\:\mathrm{select}\:\mathrm{the}\:\mathrm{incorrect}\:\mathrm{alternative}. \\ $$$$\left(\mathrm{1}\right)\:\Sigma{F}_{{y}'} \:\neq\:\mathrm{0} \\ $$$$\left(\mathrm{2}\right)\:\Sigma{F}_{{y}} \:=\:\mathrm{0} \\ $$$$\left(\mathrm{3}\right)\:\Sigma{F}_{{x}} \:=\:−{mg}\:\mathrm{sin}\:\theta \\ $$$$\left(\mathrm{4}\right)\:\Sigma{F}_{{x}'} \:<\:\mathrm{0} \\ $$

Question Number 18918 Answers: 0 Comments: 17

A bird sits on a stretched telegraph wire. The additional tension produced in the wire is (1) Zero (2) Greater than weight of the bird (3) Less than the weight of the bird (4) Equal to the weight of the bird

$$\mathrm{A}\:\mathrm{bird}\:\mathrm{sits}\:\mathrm{on}\:\mathrm{a}\:\mathrm{stretched}\:\mathrm{telegraph} \\ $$$$\mathrm{wire}.\:\mathrm{The}\:\mathrm{additional}\:\mathrm{tension}\:\mathrm{produced} \\ $$$$\mathrm{in}\:\mathrm{the}\:\mathrm{wire}\:\mathrm{is} \\ $$$$\left(\mathrm{1}\right)\:\mathrm{Zero} \\ $$$$\left(\mathrm{2}\right)\:\mathrm{Greater}\:\mathrm{than}\:\mathrm{weight}\:\mathrm{of}\:\mathrm{the}\:\mathrm{bird} \\ $$$$\left(\mathrm{3}\right)\:\mathrm{Less}\:\mathrm{than}\:\mathrm{the}\:\mathrm{weight}\:\mathrm{of}\:\mathrm{the}\:\mathrm{bird} \\ $$$$\left(\mathrm{4}\right)\:\mathrm{Equal}\:\mathrm{to}\:\mathrm{the}\:\mathrm{weight}\:\mathrm{of}\:\mathrm{the}\:\mathrm{bird} \\ $$

Question Number 18940 Answers: 0 Comments: 3

A light rope is passed over a pulley such that at its one end a block is attached, and on the other end a boy is climbing up with acceleration (g/2) relative to rope. Mass of the block is 30 kg and that of the boy is 40 kg. Find the tension and acceleration of the rope.

$$\mathrm{A}\:\mathrm{light}\:\mathrm{rope}\:\mathrm{is}\:\mathrm{passed}\:\mathrm{over}\:\mathrm{a}\:\mathrm{pulley}\:\mathrm{such} \\ $$$$\mathrm{that}\:\mathrm{at}\:\mathrm{its}\:\mathrm{one}\:\mathrm{end}\:\mathrm{a}\:\mathrm{block}\:\mathrm{is}\:\mathrm{attached}, \\ $$$$\mathrm{and}\:\mathrm{on}\:\mathrm{the}\:\mathrm{other}\:\mathrm{end}\:\mathrm{a}\:\mathrm{boy}\:\mathrm{is}\:\mathrm{climbing} \\ $$$$\mathrm{up}\:\mathrm{with}\:\mathrm{acceleration}\:\frac{{g}}{\mathrm{2}}\:\mathrm{relative}\:\mathrm{to}\:\mathrm{rope}. \\ $$$$\mathrm{Mass}\:\mathrm{of}\:\mathrm{the}\:\mathrm{block}\:\mathrm{is}\:\mathrm{30}\:\mathrm{kg}\:\mathrm{and}\:\mathrm{that}\:\mathrm{of} \\ $$$$\mathrm{the}\:\mathrm{boy}\:\mathrm{is}\:\mathrm{40}\:\mathrm{kg}.\:\mathrm{Find}\:\mathrm{the}\:\mathrm{tension}\:\mathrm{and} \\ $$$$\mathrm{acceleration}\:\mathrm{of}\:\mathrm{the}\:\mathrm{rope}. \\ $$

Question Number 18916 Answers: 0 Comments: 0

x^2 −7x+12<mod(x−4)

$${x}^{\mathrm{2}} −\mathrm{7}{x}+\mathrm{12}<{mod}\left({x}−\mathrm{4}\right) \\ $$

Question Number 18909 Answers: 0 Comments: 1

What does a_ .b_ and a_ ×b_ means ? someone please explain it.

$${What}\:{does}\:\underset{} {{a}}.\underset{} {{b}}\:\:{and}\:\underset{} {{a}}×\underset{} {{b}}\:{means}\:? \\ $$$${someone}\:{please}\:{explain}\:{it}. \\ $$

Question Number 18908 Answers: 0 Comments: 5

Why Does ∣A^→ ×B^→ ∣=ABSinθ ?

$${Why}\:{Does} \\ $$$$\mid\overset{\rightarrow} {{A}}×\overset{\rightarrow} {{B}}\mid={ABSin}\theta\:? \\ $$

Question Number 18907 Answers: 0 Comments: 3

Why Does A^→ .B^→ =ABCosθ?

$${Why}\:{Does}\: \\ $$$$\overset{\rightarrow} {{A}}.\overset{\rightarrow} {{B}}={ABCos}\theta?\: \\ $$

Question Number 18906 Answers: 1 Comments: 0

calculate (dy/dx) where y=cos^(−1) ((a+b cosx)/(b+a cosx)) (b>a)

$$\mathrm{calculate}\:\frac{\mathrm{dy}}{\mathrm{dx}}\:\:\:\mathrm{where}\: \\ $$$$\mathrm{y}=\mathrm{cos}^{−\mathrm{1}} \frac{\mathrm{a}+\mathrm{b}\:\mathrm{cosx}}{\mathrm{b}+\mathrm{a}\:\mathrm{cosx}}\:\left(\mathrm{b}>\mathrm{a}\right) \\ $$

Question Number 18905 Answers: 0 Comments: 0

prove that the differentiation of(((√(1+x^2 ))−(√(1−x^2 )))/((√(1+x^2 ))+(√(1−x^2 )))) with respect to (√(1−x^4 )) is ((√(1−x^4 ))/x^6 )

$$\mathrm{prove}\:\mathrm{that}\:\mathrm{the}\:\mathrm{differentiation} \\ $$$$\mathrm{of}\frac{\sqrt{\mathrm{1}+\mathrm{x}^{\mathrm{2}} }−\sqrt{\mathrm{1}−\mathrm{x}^{\mathrm{2}} }}{\sqrt{\mathrm{1}+\mathrm{x}^{\mathrm{2}} }+\sqrt{\mathrm{1}−\mathrm{x}^{\mathrm{2}} }}\:\:\mathrm{with}\:\mathrm{respect} \\ $$$$\mathrm{to}\:\sqrt{\mathrm{1}−\mathrm{x}^{\mathrm{4}} }\:\:\mathrm{is}\:\:\frac{\sqrt{\mathrm{1}−\mathrm{x}^{\mathrm{4}} }}{\mathrm{x}^{\mathrm{6}} } \\ $$

Question Number 18904 Answers: 1 Comments: 0

Solve the triangle in which a=((√3)+1), b=((√3)−1) and ∠C=60°.

$${Solve}\:{the}\:{triangle}\:{in}\:{which}\:{a}=\left(\sqrt{\mathrm{3}}+\mathrm{1}\right),\: \\ $$$${b}=\left(\sqrt{\mathrm{3}}−\mathrm{1}\right)\:{and}\:\angle{C}=\mathrm{60}°. \\ $$$$ \\ $$

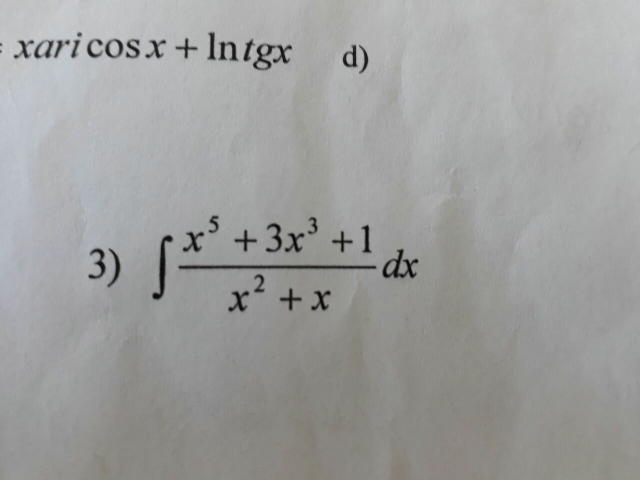
Question Number 18893 Answers: 1 Comments: 0

Find all values of x, y and k for which the system of equations sin x cos 2y = k^4 − 2k^2 + 2 cos x sin 2y = k + 1 has a solution.

$$\mathrm{Find}\:\mathrm{all}\:\mathrm{values}\:\mathrm{of}\:{x},\:{y}\:\mathrm{and}\:{k}\:\mathrm{for}\:\mathrm{which} \\ $$$$\mathrm{the}\:\mathrm{system}\:\mathrm{of}\:\mathrm{equations} \\ $$$$\mathrm{sin}\:{x}\:\mathrm{cos}\:\mathrm{2}{y}\:=\:{k}^{\mathrm{4}} \:−\:\mathrm{2}{k}^{\mathrm{2}} \:+\:\mathrm{2} \\ $$$$\mathrm{cos}\:{x}\:\mathrm{sin}\:\mathrm{2}{y}\:=\:{k}\:+\:\mathrm{1} \\ $$$$\mathrm{has}\:\mathrm{a}\:\mathrm{solution}. \\ $$

Question Number 18892 Answers: 1 Comments: 0

If the equation sin6x + cos4x = −2 have a family of nonnegative solutions x_k ′s, where 0 ≤ x_1 < x_2 < x_3 < .... < x_k < x_(k+1) ....., then the value of (1/π)Σ_(k=1) ^(1000) ∣x_(k+1) − x_k ∣ is

$$\mathrm{If}\:\mathrm{the}\:\mathrm{equation}\:\mathrm{sin6}{x}\:+\:\mathrm{cos4}{x}\:=\:−\mathrm{2}\:\mathrm{have} \\ $$$$\mathrm{a}\:\mathrm{family}\:\mathrm{of}\:\mathrm{nonnegative}\:\mathrm{solutions}\:{x}_{{k}} '\mathrm{s}, \\ $$$$\mathrm{where}\:\mathrm{0}\:\leqslant\:{x}_{\mathrm{1}} \:<\:{x}_{\mathrm{2}} \:<\:{x}_{\mathrm{3}} \:<\:....\:<\:{x}_{{k}} \:<\:{x}_{{k}+\mathrm{1}} \\ $$$$.....,\:\mathrm{then}\:\mathrm{the}\:\mathrm{value}\:\mathrm{of}\:\frac{\mathrm{1}}{\pi}\underset{{k}=\mathrm{1}} {\overset{\mathrm{1000}} {\sum}}\mid{x}_{{k}+\mathrm{1}} \:−\:{x}_{{k}} \mid\:\mathrm{is} \\ $$

Question Number 18891 Answers: 2 Comments: 0

If angles A and B satisfy (√2) cos A = cos B + cos^3 B and (√2) sin A = sin B − sin^3 B, then the value of 1620sin^2 (A − B) is

$$\mathrm{If}\:\mathrm{angles}\:{A}\:\mathrm{and}\:{B}\:\mathrm{satisfy}\:\sqrt{\mathrm{2}}\:\mathrm{cos}\:{A}\:= \\ $$$$\mathrm{cos}\:{B}\:+\:\mathrm{cos}^{\mathrm{3}} \:{B}\:\mathrm{and}\:\sqrt{\mathrm{2}}\:\mathrm{sin}\:{A}\:=\:\mathrm{sin}\:{B}\:− \\ $$$$\mathrm{sin}^{\mathrm{3}} \:{B},\:\mathrm{then}\:\mathrm{the}\:\mathrm{value}\:\mathrm{of}\:\mathrm{1620sin}^{\mathrm{2}} \left({A}\:−\:{B}\right) \\ $$$$\mathrm{is} \\ $$

Question Number 18889 Answers: 0 Comments: 2

∫ ((d((√(3x))))/(√((√x) + 7)))

$$\int\:\frac{{d}\left(\sqrt{\mathrm{3}{x}}\right)}{\sqrt{\sqrt{{x}}\:+\:\mathrm{7}}} \\ $$

Question Number 18872 Answers: 2 Comments: 0

Question Number 18871 Answers: 0 Comments: 1

Question Number 18866 Answers: 1 Comments: 0

Question Number 18864 Answers: 2 Comments: 1

Question Number 18859 Answers: 1 Comments: 0

If f(x+2)=f(x)+7 and f(1)=2; f(2)=5, then the ratio of f(150) to f(75) is

$$\mathrm{If}\:\mathrm{f}\left(\mathrm{x}+\mathrm{2}\right)=\mathrm{f}\left(\mathrm{x}\right)+\mathrm{7}\:\mathrm{and}\:\mathrm{f}\left(\mathrm{1}\right)=\mathrm{2};\:\mathrm{f}\left(\mathrm{2}\right)=\mathrm{5}, \\ $$$$\mathrm{then}\:\mathrm{the}\:\mathrm{ratio}\:\mathrm{of}\:\mathrm{f}\left(\mathrm{150}\right)\:\mathrm{to}\:\mathrm{f}\left(\mathrm{75}\right)\:\mathrm{is} \\ $$

Question Number 18854 Answers: 0 Comments: 0

lim_(x→0) sin x_x =?

$$\underset{{x}\rightarrow\mathrm{0}} {\mathrm{lim}sin}\:\underset{\mathrm{x}} {\mathrm{x}}\:\:\:\:=? \\ $$

Question Number 18847 Answers: 1 Comments: 0

In an equilateral triangle with usual notations the value of ((27r^2 R)/(r_1 r_2 r_3 )) is equal to

$$\mathrm{In}\:\mathrm{an}\:\mathrm{equilateral}\:\mathrm{triangle}\:\mathrm{with}\:\mathrm{usual} \\ $$$$\mathrm{notations}\:\mathrm{the}\:\mathrm{value}\:\mathrm{of}\:\frac{\mathrm{27}{r}^{\mathrm{2}} {R}}{{r}_{\mathrm{1}} {r}_{\mathrm{2}} {r}_{\mathrm{3}} }\:\mathrm{is}\:\mathrm{equal}\:\mathrm{to} \\ $$

Question Number 18846 Answers: 0 Comments: 0

There are two crystalline forms of PbO ; one is yellow and the other is red. The standard enthalpies of formation of these two forms are −217.3 and −219 kJ per mole respectively. Calculate the enthalpy change for the solid-solid phase transition. PbO (yellow) → PbO (red)

$$\mathrm{There}\:\mathrm{are}\:\mathrm{two}\:\mathrm{crystalline}\:\mathrm{forms}\:\mathrm{of}\:\mathrm{PbO}\:; \\ $$$$\mathrm{one}\:\mathrm{is}\:\mathrm{yellow}\:\mathrm{and}\:\mathrm{the}\:\mathrm{other}\:\mathrm{is}\:\mathrm{red}.\:\mathrm{The} \\ $$$$\mathrm{standard}\:\mathrm{enthalpies}\:\mathrm{of}\:\mathrm{formation}\:\mathrm{of} \\ $$$$\mathrm{these}\:\mathrm{two}\:\mathrm{forms}\:\mathrm{are}\:−\mathrm{217}.\mathrm{3}\:\mathrm{and}\:−\mathrm{219} \\ $$$$\mathrm{kJ}\:\mathrm{per}\:\mathrm{mole}\:\mathrm{respectively}.\:\mathrm{Calculate}\:\mathrm{the} \\ $$$$\mathrm{enthalpy}\:\mathrm{change}\:\mathrm{for}\:\mathrm{the}\:\mathrm{solid}-\mathrm{solid} \\ $$$$\mathrm{phase}\:\mathrm{transition}. \\ $$$$\mathrm{PbO}\:\left(\mathrm{yellow}\right)\:\rightarrow\:\mathrm{PbO}\:\left(\mathrm{red}\right) \\ $$

Question Number 18885 Answers: 0 Comments: 0

Question Number 18886 Answers: 0 Comments: 0

Question Number 18841 Answers: 1 Comments: 0

Pg 1885 Pg 1886 Pg 1887 Pg 1888 Pg 1889 Pg 1890 Pg 1891 Pg 1892 Pg 1893 Pg 1894

Contact: info@tinkutara.com