
AllQuestion and Answers: Page 1881
Question Number 21795 Answers: 1 Comments: 3
Question Number 21793 Answers: 0 Comments: 6
Question Number 24687 Answers: 1 Comments: 0
Question Number 24685 Answers: 0 Comments: 3
Question Number 21772 Answers: 2 Comments: 0
$${integrate} \\ $$$$\int\mathrm{2}^{\mathrm{4}{x}} {dx} \\ $$
Question Number 21771 Answers: 0 Comments: 0
Question Number 21768 Answers: 0 Comments: 2
Question Number 21766 Answers: 1 Comments: 0
Question Number 21760 Answers: 1 Comments: 0
Question Number 21759 Answers: 1 Comments: 0
Question Number 21756 Answers: 0 Comments: 0
Question Number 21754 Answers: 1 Comments: 0
Question Number 21750 Answers: 0 Comments: 2
Question Number 21747 Answers: 0 Comments: 4
Question Number 21738 Answers: 1 Comments: 0
Question Number 21784 Answers: 0 Comments: 0
Question Number 21782 Answers: 0 Comments: 0
Question Number 21781 Answers: 2 Comments: 0
Question Number 21733 Answers: 1 Comments: 0
Question Number 21732 Answers: 0 Comments: 2
Question Number 21731 Answers: 0 Comments: 0
Question Number 21722 Answers: 1 Comments: 0
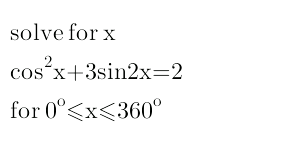
Question Number 21721 Answers: 1 Comments: 0
$$\int_{\mathrm{0}} ^{\pi/\mathrm{2}} {sin}^{\mathrm{2}} {xcos}^{\mathrm{3}} {xdx} \\ $$
Question Number 21720 Answers: 1 Comments: 0
Question Number 21713 Answers: 0 Comments: 7
Question Number 21707 Answers: 0 Comments: 3
Pg 1876 Pg 1877 Pg 1878 Pg 1879 Pg 1880 Pg 1881 Pg 1882 Pg 1883 Pg 1884 Pg 1885
