
AllQuestion and Answers: Page 1878
Question Number 22090 Answers: 2 Comments: 0

Question Number 26917 Answers: 1 Comments: 2
Question Number 22295 Answers: 1 Comments: 0
Question Number 22276 Answers: 1 Comments: 0

Question Number 22082 Answers: 1 Comments: 0
Question Number 22080 Answers: 0 Comments: 1
Question Number 22079 Answers: 0 Comments: 1
Question Number 22076 Answers: 0 Comments: 3
Question Number 22161 Answers: 0 Comments: 1
Question Number 22071 Answers: 1 Comments: 4
Question Number 26924 Answers: 1 Comments: 0
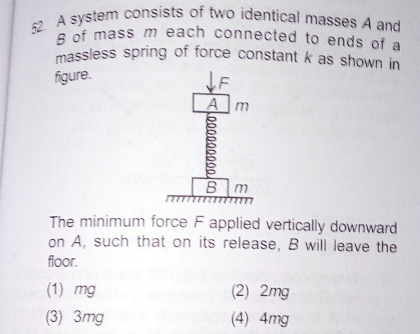
Question Number 22062 Answers: 1 Comments: 1

Question Number 22061 Answers: 1 Comments: 0
Question Number 22059 Answers: 1 Comments: 0
Question Number 22058 Answers: 1 Comments: 0
Question Number 22057 Answers: 0 Comments: 0
Question Number 22055 Answers: 0 Comments: 1
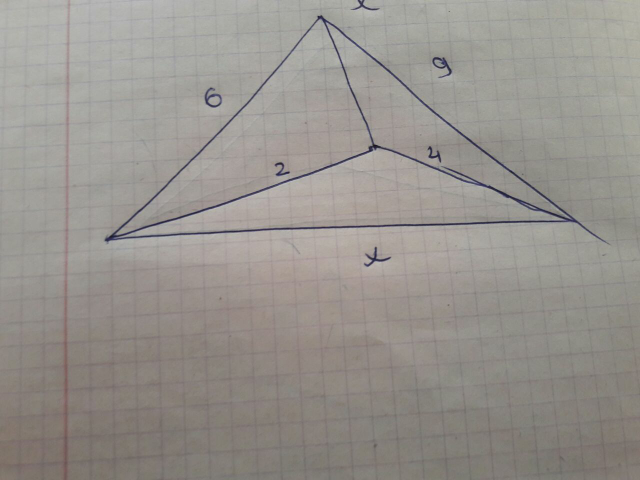
Question Number 22052 Answers: 0 Comments: 2
Question Number 22047 Answers: 2 Comments: 1
Question Number 22050 Answers: 0 Comments: 0
Question Number 22044 Answers: 1 Comments: 0
Question Number 22043 Answers: 1 Comments: 0
Question Number 22042 Answers: 1 Comments: 0
Question Number 22041 Answers: 0 Comments: 0
Question Number 22040 Answers: 0 Comments: 4
Question Number 22038 Answers: 0 Comments: 1
Pg 1873 Pg 1874 Pg 1875 Pg 1876 Pg 1877 Pg 1878 Pg 1879 Pg 1880 Pg 1881 Pg 1882
