Question and Answers Forum

AllQuestion and Answers: Page 1876

Question Number 22871 Answers: 1 Comments: 0

If f(n)=(1/n)[(n+1)(n+2)(n+3)...(n+n)]^(1/n) , then lim_(n→∞) f(n) =

$$\mathrm{If}\:\:{f}\left({n}\right)=\frac{\mathrm{1}}{{n}}\left[\left({n}+\mathrm{1}\right)\left({n}+\mathrm{2}\right)\left({n}+\mathrm{3}\right)...\left({n}+{n}\right)\right]^{\mathrm{1}/{n}} , \\ $$$$\mathrm{then}\:\:\:\underset{{n}\rightarrow\infty} {\mathrm{lim}}{f}\left({n}\right)\:= \\ $$

Question Number 22843 Answers: 1 Comments: 0

calculate the value of ∫_0 ^(1000) e^(x−[x]) dx =? where.... [x] is greatest integer functon

$${calculate}\:{the}\:{value}\:{of}\:\:\int_{\mathrm{0}} ^{\mathrm{1000}} {e}^{{x}−\left[{x}\right]} {dx}\:=? \\ $$$${where}....\:\left[{x}\right]\:{is}\:{greatest}\:{integer}\:{functon} \\ $$

Question Number 22820 Answers: 0 Comments: 2

total number of permutations of five abjects → A,A,A,B,B in a circle?

$${total}\:{number}\:{of}\:{permutations}\:{of} \\ $$$${five}\:{abjects}\:\rightarrow\:{A},{A},{A},{B},{B}\: \\ $$$${in}\:{a}\:{circle}? \\ $$

Question Number 22874 Answers: 4 Comments: 0

Question Number 22813 Answers: 1 Comments: 0

The nucleus Fe^(57) emits a γ-ray of energy 14.4 keV. If the mass of the nucleus is 56.935 u, calculate the recoil energy of nucleus.

$$\mathrm{The}\:\mathrm{nucleus}\:\mathrm{Fe}^{\mathrm{57}} \:\mathrm{emits}\:\mathrm{a}\:\gamma-\mathrm{ray}\:\mathrm{of}\:\mathrm{energy} \\ $$$$\mathrm{14}.\mathrm{4}\:\mathrm{keV}.\:\mathrm{If}\:\mathrm{the}\:\mathrm{mass}\:\mathrm{of}\:\mathrm{the}\:\mathrm{nucleus}\:\mathrm{is} \\ $$$$\mathrm{56}.\mathrm{935}\:\mathrm{u},\:\mathrm{calculate}\:\mathrm{the}\:\mathrm{recoil}\:\mathrm{energy}\:\mathrm{of} \\ $$$$\mathrm{nucleus}. \\ $$

Question Number 22797 Answers: 1 Comments: 0

He^+ in ground state is hit by photon thus exciting electron to second excited state. The energy absorbed in this process is (approx) (1) 2.18 × 10^(−14) J (2) 7.75 × 10^(−18) J (3) 4.5 × 10^(−18) J (4) 5 × 10^(−18) J

$$\mathrm{He}^{+} \:\mathrm{in}\:\mathrm{ground}\:\mathrm{state}\:\mathrm{is}\:\mathrm{hit}\:\mathrm{by}\:\mathrm{photon} \\ $$$$\mathrm{thus}\:\mathrm{exciting}\:\mathrm{electron}\:\mathrm{to}\:\mathrm{second}\:\mathrm{excited} \\ $$$$\mathrm{state}.\:\mathrm{The}\:\mathrm{energy}\:\mathrm{absorbed}\:\mathrm{in}\:\mathrm{this} \\ $$$$\mathrm{process}\:\mathrm{is}\:\left(\mathrm{approx}\right) \\ $$$$\left(\mathrm{1}\right)\:\mathrm{2}.\mathrm{18}\:×\:\mathrm{10}^{−\mathrm{14}} \:\mathrm{J} \\ $$$$\left(\mathrm{2}\right)\:\mathrm{7}.\mathrm{75}\:×\:\mathrm{10}^{−\mathrm{18}} \:\mathrm{J} \\ $$$$\left(\mathrm{3}\right)\:\mathrm{4}.\mathrm{5}\:×\:\mathrm{10}^{−\mathrm{18}} \:\mathrm{J} \\ $$$$\left(\mathrm{4}\right)\:\mathrm{5}\:×\:\mathrm{10}^{−\mathrm{18}} \:\mathrm{J} \\ $$

Question Number 22787 Answers: 0 Comments: 2

sin^(−1) (sin 10)=10 or 3π−10 Ans is 3π−10 How

$$\mathrm{sin}^{−\mathrm{1}} \left(\mathrm{sin}\:\mathrm{10}\right)=\mathrm{10}\:\mathrm{or}\:\mathrm{3}\pi−\mathrm{10} \\ $$$$\mathrm{Ans}\:\mathrm{is}\:\mathrm{3}\pi−\mathrm{10}\:\:\:\mathrm{How} \\ $$

Question Number 22782 Answers: 0 Comments: 6

Successive ionisation energies of element is 738, 1450, 10540, 13630 kJ/mole respectively. The element is (1) Na (2) Mg (3) Al (4) K

$$\mathrm{Successive}\:\mathrm{ionisation}\:\mathrm{energies}\:\mathrm{of} \\ $$$$\mathrm{element}\:\mathrm{is}\:\mathrm{738},\:\mathrm{1450},\:\mathrm{10540},\:\mathrm{13630} \\ $$$$\mathrm{kJ}/\mathrm{mole}\:\mathrm{respectively}.\:\mathrm{The}\:\mathrm{element}\:\mathrm{is} \\ $$$$\left(\mathrm{1}\right)\:\mathrm{Na} \\ $$$$\left(\mathrm{2}\right)\:\mathrm{Mg} \\ $$$$\left(\mathrm{3}\right)\:\mathrm{Al} \\ $$$$\left(\mathrm{4}\right)\:\mathrm{K} \\ $$

Question Number 22778 Answers: 0 Comments: 2

Question Number 22769 Answers: 1 Comments: 0

write to geometry form (3/5)+(4/5)i help plz

$$\boldsymbol{\mathrm{write}}\:\boldsymbol{\mathrm{to}}\:\boldsymbol{\mathrm{geometry}}\:\boldsymbol{\mathrm{form}} \\ $$$$\:\frac{\mathrm{3}}{\mathrm{5}}+\frac{\mathrm{4}}{\mathrm{5}}\boldsymbol{\mathrm{i}} \\ $$$$ \\ $$$$\boldsymbol{\mathrm{help}}\:\boldsymbol{\mathrm{plz}}\: \\ $$

Question Number 22768 Answers: 1 Comments: 2

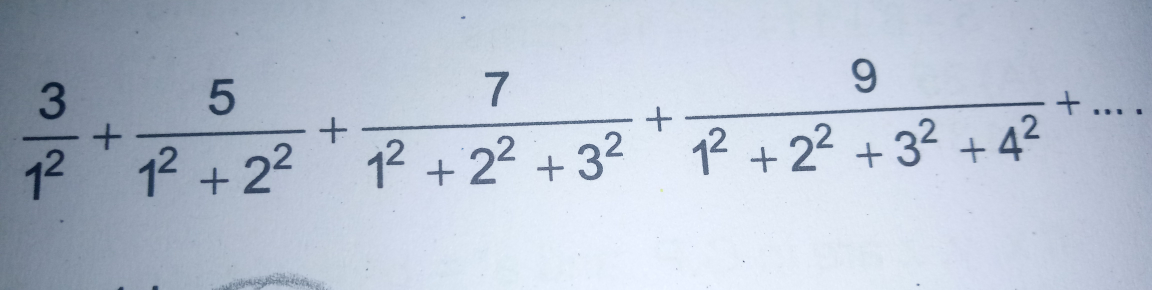
Question Number 22745 Answers: 1 Comments: 0

The number of solutions of the equation log_(101) log_7 ((√(x+7))+(√x))=0 is

$$\mathrm{The}\:\mathrm{number}\:\mathrm{of}\:\mathrm{solutions}\:\mathrm{of}\:\mathrm{the}\: \\ $$$$\mathrm{equation}\:\:\mathrm{log}_{\mathrm{101}} \mathrm{log}_{\mathrm{7}} \left(\sqrt{{x}+\mathrm{7}}+\sqrt{{x}}\right)=\mathrm{0}\:\mathrm{is} \\ $$

Question Number 22744 Answers: 0 Comments: 1

How can i copy and paste from this keyboard to other apps in my mobile? i can copy but can not getting paste in other apps. what to do?

$$\mathrm{How}\:\mathrm{can}\:\mathrm{i}\:\mathrm{copy}\:\mathrm{and}\:\mathrm{paste}\:\mathrm{from}\:\mathrm{this}\: \\ $$$$\mathrm{keyboard}\:\mathrm{to}\:\mathrm{other}\:\mathrm{apps}\:\mathrm{in}\:\mathrm{my}\:\mathrm{mobile}?\:\mathrm{i}\:\mathrm{can}\:\mathrm{copy}\:\mathrm{but}\: \\ $$$$\mathrm{can}\:\mathrm{not}\:\mathrm{getting}\:\mathrm{paste}\:\mathrm{in}\:\mathrm{other}\:\mathrm{apps}.\: \\ $$$$\mathrm{what}\:\mathrm{to}\:\mathrm{do}? \\ $$$$ \\ $$

Question Number 22743 Answers: 1 Comments: 0

The Enthalpy of neutralization of acetic acid and sodium hydroxide is −55.4 kJ. What is the enthalpy of ionisation of acetic acid?

$$\mathrm{The}\:\mathrm{Enthalpy}\:\mathrm{of}\:\mathrm{neutralization}\:\mathrm{of} \\ $$$$\mathrm{acetic}\:\mathrm{acid}\:\mathrm{and}\:\mathrm{sodium}\:\mathrm{hydroxide}\:\mathrm{is} \\ $$$$−\mathrm{55}.\mathrm{4}\:\mathrm{kJ}.\:\mathrm{What}\:\mathrm{is}\:\mathrm{the}\:\mathrm{enthalpy}\:\mathrm{of} \\ $$$$\mathrm{ionisation}\:\mathrm{of}\:\mathrm{acetic}\:\mathrm{acid}? \\ $$

Question Number 22742 Answers: 2 Comments: 0

Question Number 22740 Answers: 0 Comments: 10

Which is the best book for +1 trigonometry?

$$\mathrm{Which}\:\mathrm{is}\:\mathrm{the}\:\mathrm{best}\:\mathrm{book}\:\mathrm{for} \\ $$$$+\mathrm{1}\:\mathrm{trigonometry}? \\ $$

Question Number 22739 Answers: 0 Comments: 0

If (1 + x)^n = C_0 + C_1 x + C_2 x^2 + C_3 x^3 + ... + C_n x^n , Prove that ΣΣ_(0≤i<j≤n) (i + j)C_i C_j = n(2^(2n−1) − (1/2)^(2n) C_n )

$${If}\:\left(\mathrm{1}\:+\:{x}\right)^{{n}} \:=\:{C}_{\mathrm{0}} \:+\:{C}_{\mathrm{1}} {x}\:+\:{C}_{\mathrm{2}} {x}^{\mathrm{2}} \:+\:{C}_{\mathrm{3}} {x}^{\mathrm{3}} \\ $$$$+\:...\:+\:{C}_{{n}} {x}^{{n}} , \\ $$$${Prove}\:{that}\:\underset{\mathrm{0}\leqslant{i}<{j}\leqslant{n}} {\Sigma\Sigma}\left({i}\:+\:{j}\right){C}_{{i}} {C}_{{j}} \:= \\ $$$${n}\left(\mathrm{2}^{\mathrm{2}{n}−\mathrm{1}} \:−\:\frac{\mathrm{1}}{\mathrm{2}}\:^{\mathrm{2}{n}} {C}_{{n}} \right) \\ $$

Question Number 22714 Answers: 1 Comments: 0

Question Number 22703 Answers: 1 Comments: 1

Question Number 22701 Answers: 2 Comments: 0

Question Number 22700 Answers: 0 Comments: 0

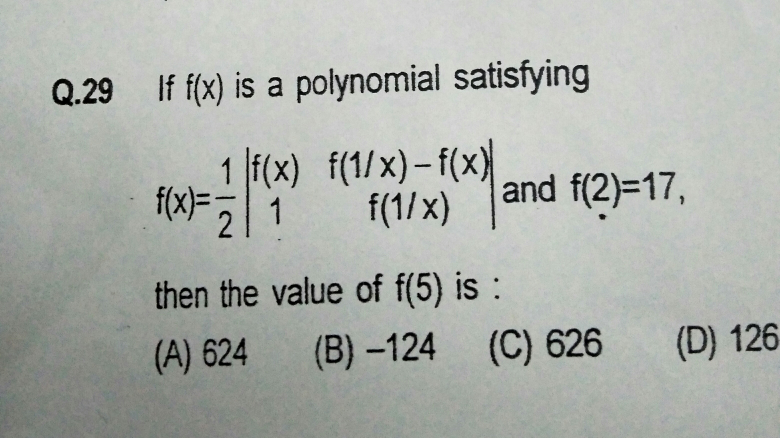
Question Number 22692 Answers: 1 Comments: 1

Question Number 22689 Answers: 1 Comments: 0

Question Number 22679 Answers: 0 Comments: 3

Maximum covalency of nitrogen is equal to

$$\mathrm{Maximum}\:\mathrm{covalency}\:\mathrm{of}\:\mathrm{nitrogen}\:\mathrm{is} \\ $$$$\mathrm{equal}\:\mathrm{to} \\ $$

Question Number 22678 Answers: 0 Comments: 0

∫ ((9x^4 + 12x(x^3 + 1))/(2(x^3 + 1)^(1/2) )) dx

$$\int\:\frac{\mathrm{9x}^{\mathrm{4}} \:+\:\mathrm{12x}\left(\mathrm{x}^{\mathrm{3}} \:+\:\mathrm{1}\right)}{\mathrm{2}\left(\mathrm{x}^{\mathrm{3}} \:+\:\mathrm{1}\right)^{\mathrm{1}/\mathrm{2}} }\:\mathrm{dx} \\ $$

Question Number 22661 Answers: 1 Comments: 1

Pg 1871 Pg 1872 Pg 1873 Pg 1874 Pg 1875 Pg 1876 Pg 1877 Pg 1878 Pg 1879 Pg 1880

Contact: [email protected]