
AllQuestion and Answers: Page 1875
Question Number 22975 Answers: 0 Comments: 5

Question Number 22972 Answers: 0 Comments: 0
$${Can}\:{anyone}\:{please}\:{solve}\:{question} \\ $$$${number}\:\mathrm{22956} \\ $$
Question Number 22993 Answers: 2 Comments: 0
Question Number 22968 Answers: 0 Comments: 2

Question Number 22959 Answers: 0 Comments: 0
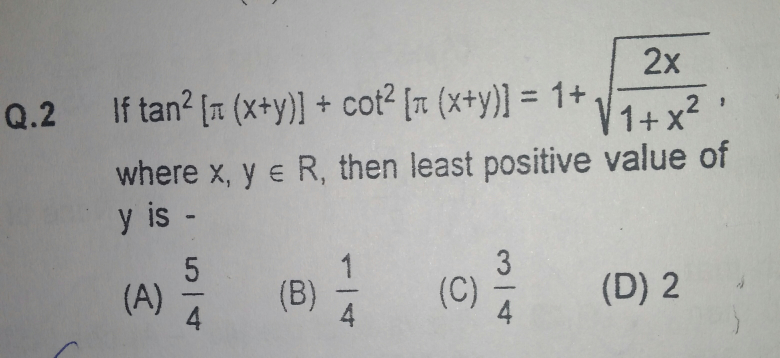
Question Number 22947 Answers: 0 Comments: 0
Question Number 22946 Answers: 2 Comments: 0
Question Number 22945 Answers: 0 Comments: 0

Question Number 22940 Answers: 0 Comments: 1

Question Number 22939 Answers: 1 Comments: 0

Question Number 22937 Answers: 0 Comments: 0
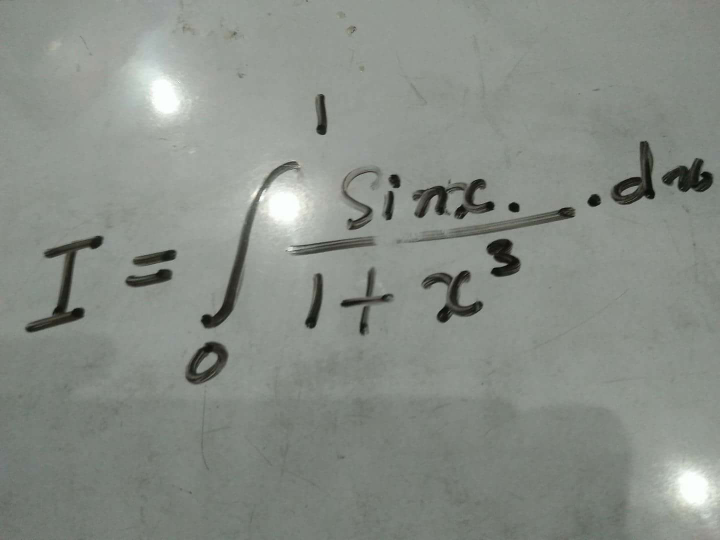
Question Number 22930 Answers: 1 Comments: 0

Question Number 22929 Answers: 1 Comments: 0

Question Number 22928 Answers: 1 Comments: 0

Question Number 22956 Answers: 1 Comments: 4

Question Number 22923 Answers: 1 Comments: 0

Question Number 22922 Answers: 0 Comments: 0

Question Number 22896 Answers: 0 Comments: 1
Question Number 22941 Answers: 1 Comments: 3

Question Number 22893 Answers: 1 Comments: 0
Question Number 22892 Answers: 0 Comments: 3
Question Number 22883 Answers: 1 Comments: 1
Question Number 22881 Answers: 0 Comments: 3
Question Number 22879 Answers: 1 Comments: 0
Question Number 22872 Answers: 1 Comments: 4

Question Number 22856 Answers: 0 Comments: 1
$$\mathrm{solve}:\:\mathrm{sin}\left({x}\right)=\mathrm{2},\:\:\:{x}\in\mathbb{C} \\ $$
Pg 1870 Pg 1871 Pg 1872 Pg 1873 Pg 1874 Pg 1875 Pg 1876 Pg 1877 Pg 1878 Pg 1879
