
AllQuestion and Answers: Page 1869
Question Number 23752 Answers: 1 Comments: 0
$$\int_{\mathrm{1}} ^{\mathrm{2}} {x}^{\mathrm{3}} +\mathrm{1}=? \\ $$
Question Number 23785 Answers: 2 Comments: 0
Question Number 23748 Answers: 1 Comments: 1

Question Number 23741 Answers: 1 Comments: 0
$$\left(\mathrm{1}+{i}\right)\left(\mathrm{2}+{i}\right) \\ $$
Question Number 23715 Answers: 0 Comments: 0
Question Number 23711 Answers: 1 Comments: 0
Question Number 23707 Answers: 1 Comments: 4
Question Number 24506 Answers: 0 Comments: 8
Question Number 23700 Answers: 0 Comments: 3
Question Number 23694 Answers: 0 Comments: 0
Question Number 23688 Answers: 1 Comments: 0
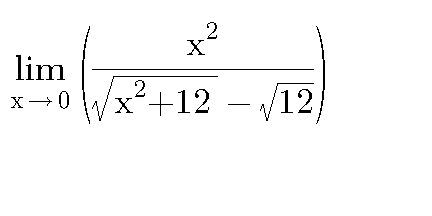
Question Number 23687 Answers: 1 Comments: 0
Question Number 23686 Answers: 0 Comments: 0
Question Number 23683 Answers: 0 Comments: 0

Question Number 23682 Answers: 0 Comments: 0

Question Number 23679 Answers: 2 Comments: 0

Question Number 23718 Answers: 0 Comments: 1
Question Number 23739 Answers: 0 Comments: 3

Question Number 23666 Answers: 2 Comments: 1
Question Number 23677 Answers: 0 Comments: 0
Question Number 23663 Answers: 1 Comments: 3
Question Number 23657 Answers: 0 Comments: 1
Question Number 23648 Answers: 1 Comments: 0
Question Number 23644 Answers: 0 Comments: 0
Question Number 23645 Answers: 0 Comments: 1
Question Number 23632 Answers: 0 Comments: 9

Pg 1864 Pg 1865 Pg 1866 Pg 1867 Pg 1868 Pg 1869 Pg 1870 Pg 1871 Pg 1872 Pg 1873
