
AllQuestion and Answers: Page 1867
Question Number 24023 Answers: 0 Comments: 0
Question Number 24022 Answers: 1 Comments: 0
Question Number 24025 Answers: 1 Comments: 4

Question Number 23996 Answers: 1 Comments: 0
Question Number 24010 Answers: 0 Comments: 0
Question Number 23984 Answers: 2 Comments: 0
Question Number 23960 Answers: 1 Comments: 4

Question Number 23957 Answers: 0 Comments: 0
Question Number 23968 Answers: 0 Comments: 3
$${Prove}\:{that}\:{n}\:{and}\:\mathrm{2}{n}−\mathrm{1}\:{are}\:{coprime}. \\ $$
Question Number 23972 Answers: 0 Comments: 0
Question Number 23953 Answers: 0 Comments: 4
Question Number 23940 Answers: 0 Comments: 2
Question Number 23939 Answers: 0 Comments: 0
Question Number 23937 Answers: 1 Comments: 1
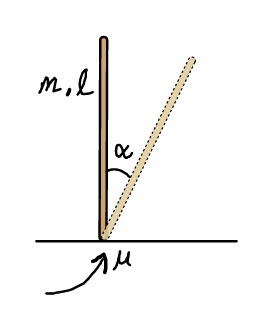
Question Number 23928 Answers: 0 Comments: 4
Question Number 23932 Answers: 1 Comments: 0
Question Number 23922 Answers: 1 Comments: 0
Question Number 23920 Answers: 1 Comments: 1
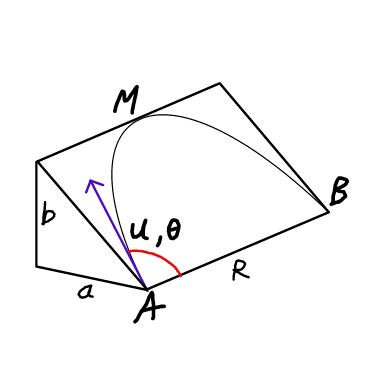
Question Number 23981 Answers: 1 Comments: 0
Question Number 23925 Answers: 0 Comments: 0
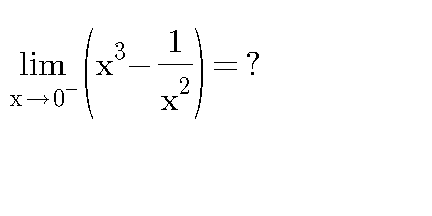
Question Number 23900 Answers: 0 Comments: 0
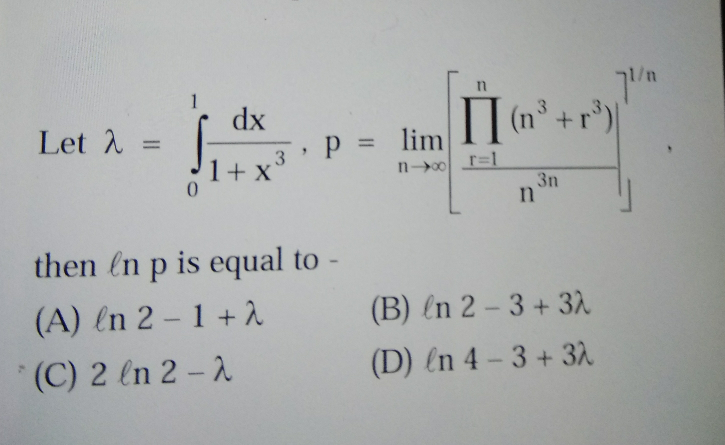
Question Number 23897 Answers: 1 Comments: 3
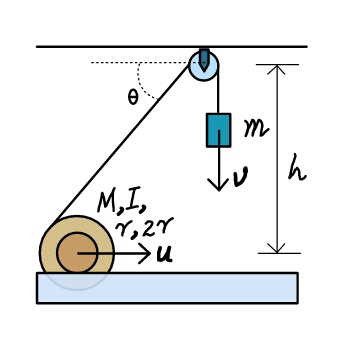
Question Number 23891 Answers: 0 Comments: 3

Question Number 23883 Answers: 0 Comments: 0
$${plz}\:{anyone}\:\:\:{answer}\:{the}\:{question}\:\mathrm{23870}\:.{plz}\:{plz}\:{plz}..... \\ $$
Question Number 23871 Answers: 0 Comments: 0
Question Number 23870 Answers: 0 Comments: 0
Pg 1862 Pg 1863 Pg 1864 Pg 1865 Pg 1866 Pg 1867 Pg 1868 Pg 1869 Pg 1870 Pg 1871
