
AllQuestion and Answers: Page 1854
Question Number 25273 Answers: 0 Comments: 0
Question Number 25254 Answers: 1 Comments: 0
Question Number 25253 Answers: 1 Comments: 1
Question Number 25252 Answers: 1 Comments: 0
Question Number 25251 Answers: 0 Comments: 1
Question Number 25246 Answers: 1 Comments: 0
Question Number 25245 Answers: 2 Comments: 0
Question Number 25278 Answers: 0 Comments: 4
Question Number 25279 Answers: 2 Comments: 0
Question Number 25237 Answers: 0 Comments: 1
Question Number 25236 Answers: 0 Comments: 1

Question Number 25230 Answers: 1 Comments: 0
Question Number 25229 Answers: 0 Comments: 1
$$\int\frac{\mathrm{1}}{\sqrt{{x}^{\mathrm{2}} +\mathrm{1}}}{dx} \\ $$
Question Number 25224 Answers: 1 Comments: 0
$$\int\left(\mathrm{2}{x}−\mathrm{1}\right)\sqrt{{x}×{x}−{x}+\mathrm{1}\:\:\:{dx}} \\ $$
Question Number 25226 Answers: 1 Comments: 0
Question Number 25221 Answers: 1 Comments: 0
Question Number 25215 Answers: 0 Comments: 1

Question Number 25209 Answers: 1 Comments: 0
$$\int{cosec}\sqrt{\mathrm{4}{x}^{\mathrm{2}} }{dx} \\ $$$$ \\ $$
Question Number 25203 Answers: 1 Comments: 1
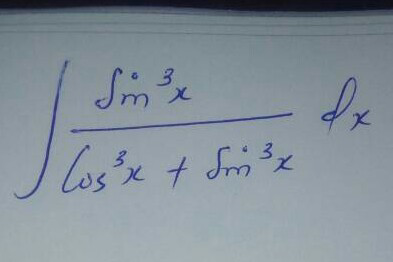
Question Number 25201 Answers: 1 Comments: 0
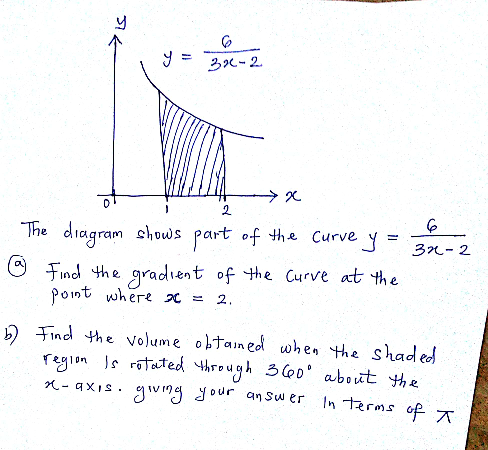
Question Number 25200 Answers: 1 Comments: 0
Question Number 25199 Answers: 1 Comments: 1
Question Number 25198 Answers: 0 Comments: 0
Question Number 25191 Answers: 0 Comments: 3
Question Number 25188 Answers: 0 Comments: 1
Question Number 25187 Answers: 0 Comments: 1
Pg 1849 Pg 1850 Pg 1851 Pg 1852 Pg 1853 Pg 1854 Pg 1855 Pg 1856 Pg 1857 Pg 1858
