Question and Answers Forum

AllQuestion and Answers: Page 1851

Question Number 25588 Answers: 1 Comments: 1

lim_(x→0) (((x−tgx)/(x−sinx)))=? l′hopital role not allowed!

$$\underset{{x}\rightarrow\mathrm{0}} {\mathrm{lim}}\left(\frac{\boldsymbol{{x}}−\boldsymbol{{tgx}}}{\boldsymbol{{x}}−\boldsymbol{{sinx}}}\right)=? \\ $$$$\boldsymbol{{l}}'\boldsymbol{{hopital}}\:\boldsymbol{{role}}\:\boldsymbol{{not}}\:\boldsymbol{{allowed}}! \\ $$

Question Number 25587 Answers: 0 Comments: 0

∫ (dx/(1+lnx))=?

$$\int\:\:\frac{\boldsymbol{{dx}}}{\mathrm{1}+\boldsymbol{{lnx}}}=? \\ $$

Question Number 25578 Answers: 0 Comments: 0

3 men A,B and C can complete a work in such a way that A works for all the days, B works for 1st and 2nd day and C works for 3rd, 4th and 5th day. If B and C can do as much work in two days as a alone does in 3 days. If B and C can complete the work without tbe help of A in 6 days then how many dahs A alone do the work?

$$\mathrm{3}\:\mathrm{men}\:\mathrm{A},\mathrm{B}\:\mathrm{and}\:\mathrm{C}\:\mathrm{can}\:\mathrm{complete}\:\mathrm{a} \\ $$$$\mathrm{work}\:\mathrm{in}\:\mathrm{such}\:\mathrm{a}\:\mathrm{way}\:\mathrm{that}\:\mathrm{A}\:\mathrm{works}\:\mathrm{for} \\ $$$$\mathrm{all}\:\mathrm{the}\:\mathrm{days},\:\mathrm{B}\:\mathrm{works}\:\mathrm{for}\:\mathrm{1st}\:\mathrm{and}\:\mathrm{2nd} \\ $$$$\mathrm{day}\:\mathrm{and}\:\mathrm{C}\:\mathrm{works}\:\mathrm{for}\:\mathrm{3rd},\:\mathrm{4th}\:\mathrm{and}\:\mathrm{5th} \\ $$$$\mathrm{day}.\:\mathrm{If}\:\mathrm{B}\:\mathrm{and}\:\mathrm{C}\:\mathrm{can}\:\mathrm{do}\:\mathrm{as}\:\mathrm{much}\:\mathrm{work} \\ $$$$\mathrm{in}\:\mathrm{two}\:\mathrm{days}\:\mathrm{as}\:\mathrm{a}\:\mathrm{alone}\:\mathrm{does}\:\mathrm{in}\:\mathrm{3}\:\mathrm{days}. \\ $$$$\mathrm{If}\:\mathrm{B}\:\mathrm{and}\:\mathrm{C}\:\mathrm{can}\:\mathrm{complete}\:\mathrm{the}\:\mathrm{work}\: \\ $$$$\mathrm{without}\:\mathrm{tbe}\:\mathrm{help}\:\mathrm{of}\:\mathrm{A}\:\mathrm{in}\:\mathrm{6}\:\mathrm{days}\:\mathrm{then}\: \\ $$$$\mathrm{how}\:\mathrm{many}\:\mathrm{dahs}\:\mathrm{A}\:\mathrm{alone}\:\mathrm{do}\:\mathrm{the}\:\mathrm{work}? \\ $$

Question Number 25572 Answers: 1 Comments: 0

Solve the differential equation: y′ = cosh(x+y)

$${Solve}\:{the}\:{differential}\:{equation}: \\ $$$${y}'\:=\:{cosh}\left({x}+{y}\right) \\ $$

Question Number 25569 Answers: 0 Comments: 8

if y =(sin^(−1) x)^2 ,check whether (1−x^2 )y_(n+2) −(2n+1)xy_(n+1) +n^2 y_n =0 or not.

$${if}\:{y}\:=\left({sin}^{−\mathrm{1}} {x}\right)^{\mathrm{2}} ,{check}\:{whether} \\ $$$$\left(\mathrm{1}−{x}^{\mathrm{2}} \right){y}_{{n}+\mathrm{2}} −\left(\mathrm{2}{n}+\mathrm{1}\right){xy}_{{n}+\mathrm{1}} +{n}^{\mathrm{2}} {y}_{{n}} =\mathrm{0} \\ $$$${or}\:{not}. \\ $$

Question Number 25567 Answers: 2 Comments: 1

if y( sinx)^((sinx)^((sinx).^.^.^(.∞) ) ) find dy/dx.

$${if}\:{y}\left(\:{sinx}\right)^{\left({sinx}\right)^{\left({sinx}\right).^{.^{.^{.\infty} } } } } \\ $$$${find}\:{dy}/{dx}. \\ $$

Question Number 25559 Answers: 0 Comments: 2

(1) In a single throw of three dice,find the probability of getting a total of (i) 4 (ii) at most 4 (iii) atleast 4

$$\left(\mathrm{1}\right)\:\mathrm{In}\:\mathrm{a}\:\mathrm{single}\:\mathrm{throw}\:\mathrm{of}\:\mathrm{three}\: \\ $$$$\mathrm{dice},\mathrm{find}\:\mathrm{the}\:\mathrm{probability}\:\mathrm{of}\:\mathrm{getting} \\ $$$$\mathrm{a}\:\mathrm{total}\:\mathrm{of} \\ $$$$\left(\mathrm{i}\right)\:\mathrm{4} \\ $$$$\left(\mathrm{ii}\right)\:\mathrm{at}\:\mathrm{most}\:\mathrm{4} \\ $$$$\left(\mathrm{iii}\right)\:\mathrm{atleast}\:\mathrm{4} \\ $$

Question Number 25549 Answers: 1 Comments: 0

The mean weights of three groups of students consisting of 16, 18 and 20 students are 40.5kg, 42.50kg and 45.00kg respectively. What is the mean weight of all the students?

$$\mathrm{The}\:\mathrm{mean}\:\mathrm{weights}\:\mathrm{of}\:\mathrm{three}\:\mathrm{groups}\:\mathrm{of}\:\mathrm{students} \\ $$$$\mathrm{consisting}\:\mathrm{of}\:\mathrm{16},\:\mathrm{18}\:\mathrm{and}\:\mathrm{20}\:\mathrm{students}\:\mathrm{are}\:\mathrm{40}.\mathrm{5kg},\:\mathrm{42}.\mathrm{50kg} \\ $$$$\mathrm{and}\:\mathrm{45}.\mathrm{00kg}\:\mathrm{respectively}.\:\mathrm{What}\:\mathrm{is}\:\mathrm{the}\:\mathrm{mean}\:\mathrm{weight} \\ $$$$\mathrm{of}\:\mathrm{all}\:\mathrm{the}\:\mathrm{students}? \\ $$

Question Number 25543 Answers: 2 Comments: 4

Question Number 25536 Answers: 1 Comments: 0

If x = 2sec(3t) and y = 4tan(3t), Show that y = 4(x^2 − 4)

$$\mathrm{If}\:\:\:\mathrm{x}\:=\:\mathrm{2sec}\left(\mathrm{3t}\right)\:\:\mathrm{and}\:\:\mathrm{y}\:=\:\mathrm{4tan}\left(\mathrm{3t}\right),\:\:\:\mathrm{Show}\:\mathrm{that}\:\:\:\:\mathrm{y}\:=\:\mathrm{4}\left(\mathrm{x}^{\mathrm{2}} \:−\:\mathrm{4}\right) \\ $$

Question Number 25533 Answers: 1 Comments: 0

Three sets of beans l, m, and n are sold for5 for $5.00, $15.00 and $17.50 respectively per kg. If they are mixed in the ratio of 1:3:2, what is the cost per kg of the mixture?×

$${Three}\:{sets}\:{of}\:{beans}\:{l},\:{m},\:{and}\:{n}\:{are}\:{sold}\:{for}\mathrm{5} \\ $$$${for}\:\$\mathrm{5}.\mathrm{00},\:\$\mathrm{15}.\mathrm{00}\:{and}\:\$\mathrm{17}.\mathrm{50}\:{respectively} \\ $$$${per}\:{kg}.\:{If}\:{they}\:{are}\:{mixed}\:{in}\:{the}\:{ratio}\:{of} \\ $$$$\mathrm{1}:\mathrm{3}:\mathrm{2},\:{what}\:{is}\:{the}\:{cost}\:{per}\:{kg}\:{of}\:{the}\:{mixture}?× \\ $$

Question Number 25716 Answers: 0 Comments: 0

Question Number 25519 Answers: 2 Comments: 1

Question Number 25520 Answers: 2 Comments: 1

Question Number 25509 Answers: 0 Comments: 1

Question Number 25521 Answers: 1 Comments: 0

Question Number 25528 Answers: 2 Comments: 1

Question Number 25488 Answers: 2 Comments: 3

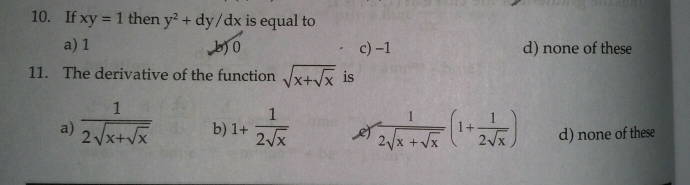
Question Number 25495 Answers: 0 Comments: 1

Question Number 25738 Answers: 1 Comments: 0

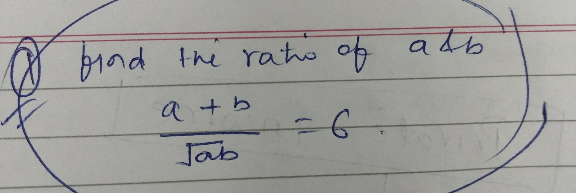
Question Number 25736 Answers: 0 Comments: 0

Question Number 25483 Answers: 1 Comments: 0

valute ∫(1/((x−1)^2 ))(/((x^2 +4)))dx

$${valute}\:\int\frac{\mathrm{1}}{\left({x}−\mathrm{1}\right)^{\mathrm{2}} }\frac{}{\left({x}^{\mathrm{2}} +\mathrm{4}\right)}{dx} \\ $$

Question Number 25479 Answers: 1 Comments: 0

Question Number 25482 Answers: 1 Comments: 3

Question Number 25477 Answers: 0 Comments: 0

((1+x)/2)=x−3+(5/x) LCM=( 2)(x) multiply each step by 2x (2)(x)(((1+x)/2))=(2)(x)(x−3)+(2)(x)((5/x)) (x)(1+x)=2x(x−3)+(2)(5) x+x^2 =2x^2 −6x+10 move all equations to LHS 2x^2 −x^2 −6x−x+10=0 x^2 −5x+10=0 x=((5±(√(25−40)))/2)=((5±(√(−15)))/2)=(1/2)(5±i(√(15)))

$$\frac{\mathrm{1}+{x}}{\mathrm{2}}={x}−\mathrm{3}+\frac{\mathrm{5}}{{x}} \\ $$$${LCM}=\left(\:\mathrm{2}\right)\left({x}\right) \\ $$$${multiply}\:{each}\:{step}\:{by}\:\mathrm{2}{x} \\ $$$$ \\ $$$$\left(\mathrm{2}\right)\left({x}\right)\left(\frac{\mathrm{1}+{x}}{\mathrm{2}}\right)=\left(\mathrm{2}\right)\left({x}\right)\left({x}−\mathrm{3}\right)+\left(\mathrm{2}\right)\left({x}\right)\left(\frac{\mathrm{5}}{{x}}\right) \\ $$$$ \\ $$$$\left({x}\right)\left(\mathrm{1}+{x}\right)=\mathrm{2}{x}\left({x}−\mathrm{3}\right)+\left(\mathrm{2}\right)\left(\mathrm{5}\right)\:\:\:\:\:\:\:\:\:\:\: \\ $$$${x}+{x}^{\mathrm{2}} =\mathrm{2}{x}^{\mathrm{2}} −\mathrm{6}{x}+\mathrm{10} \\ $$$${move}\:{all}\:{equations}\:{to}\:{LHS} \\ $$$$\mathrm{2}{x}^{\mathrm{2}} −{x}^{\mathrm{2}} −\mathrm{6}{x}−{x}+\mathrm{10}=\mathrm{0} \\ $$$${x}^{\mathrm{2}} −\mathrm{5}{x}+\mathrm{10}=\mathrm{0} \\ $$$${x}=\frac{\mathrm{5}\pm\sqrt{\mathrm{25}−\mathrm{40}}}{\mathrm{2}}=\frac{\mathrm{5}\pm\sqrt{−\mathrm{15}}}{\mathrm{2}}=\frac{\mathrm{1}}{\mathrm{2}}\left(\mathrm{5}\pm{i}\sqrt{\mathrm{15}}\right) \\ $$

Question Number 25476 Answers: 1 Comments: 0

convert 1234.24_8 to base 10

$${convert}\:\mathrm{1234}.\mathrm{24}_{\mathrm{8}} \:{to}\:{base}\:\mathrm{10} \\ $$

Pg 1846 Pg 1847 Pg 1848 Pg 1849 Pg 1850 Pg 1851 Pg 1852 Pg 1853 Pg 1854 Pg 1855

Contact: info@tinkutara.com