
AllQuestion and Answers: Page 1848
Question Number 25852 Answers: 0 Comments: 1
Question Number 25851 Answers: 0 Comments: 1
Question Number 25865 Answers: 1 Comments: 0
Question Number 25846 Answers: 0 Comments: 3
Question Number 25845 Answers: 2 Comments: 0
Question Number 25842 Answers: 2 Comments: 2
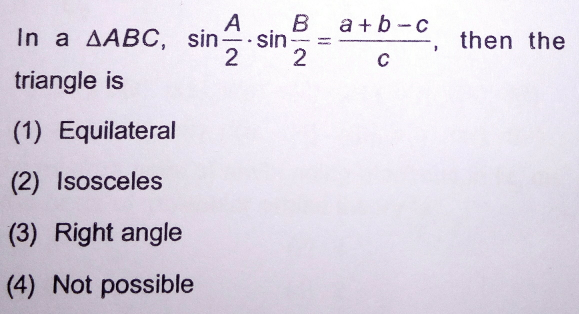
Question Number 25838 Answers: 0 Comments: 4

Question Number 25837 Answers: 1 Comments: 0
Question Number 25854 Answers: 1 Comments: 0
$${find}\:\frac{{dy}}{{dx}}\:{for}\:{y}=\sqrt{{x}+\sqrt{{x}+\sqrt{{x}+\sqrt{{x}.........}}}} \\ $$
Question Number 25828 Answers: 2 Comments: 1
Question Number 25825 Answers: 1 Comments: 0
Question Number 25824 Answers: 0 Comments: 0
Question Number 25823 Answers: 0 Comments: 1
Question Number 25822 Answers: 0 Comments: 0
Question Number 25821 Answers: 0 Comments: 0
Question Number 25814 Answers: 1 Comments: 0
Question Number 25811 Answers: 0 Comments: 1
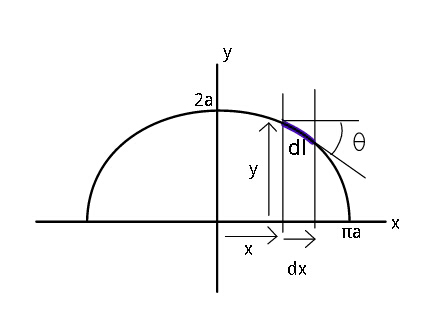
Question Number 25800 Answers: 2 Comments: 0
Question Number 25796 Answers: 0 Comments: 0
Question Number 26411 Answers: 1 Comments: 0
Question Number 26410 Answers: 1 Comments: 0
Question Number 25787 Answers: 0 Comments: 2
$$\mathrm{2}^{{x}} ={x}^{\mathrm{2}\:} ,{hence}\:{x}=\mathrm{2}\:.\:{prove} \\ $$
Question Number 25786 Answers: 1 Comments: 0
Question Number 25783 Answers: 1 Comments: 0
Question Number 26952 Answers: 1 Comments: 0
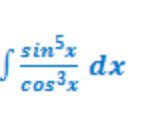
Question Number 26951 Answers: 1 Comments: 0

Pg 1843 Pg 1844 Pg 1845 Pg 1846 Pg 1847 Pg 1848 Pg 1849 Pg 1850 Pg 1851 Pg 1852
