
AllQuestion and Answers: Page 1846
Question Number 26046 Answers: 1 Comments: 0
Question Number 26042 Answers: 0 Comments: 2
Question Number 26040 Answers: 0 Comments: 0

Question Number 26110 Answers: 0 Comments: 0
Question Number 26036 Answers: 1 Comments: 0
Question Number 26031 Answers: 0 Comments: 0
Question Number 26024 Answers: 0 Comments: 0
Question Number 26023 Answers: 0 Comments: 0
Question Number 26021 Answers: 1 Comments: 1
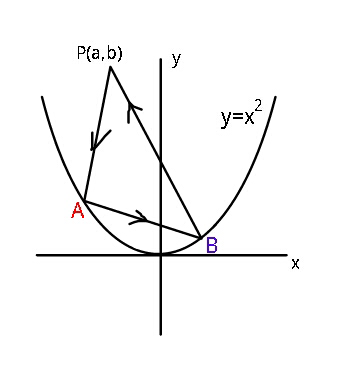
Question Number 26020 Answers: 0 Comments: 0
Question Number 26019 Answers: 0 Comments: 0

Question Number 26008 Answers: 2 Comments: 0

Question Number 26007 Answers: 1 Comments: 0

Question Number 25998 Answers: 1 Comments: 1

Question Number 26009 Answers: 1 Comments: 0

Question Number 25985 Answers: 1 Comments: 0
Question Number 26097 Answers: 0 Comments: 0
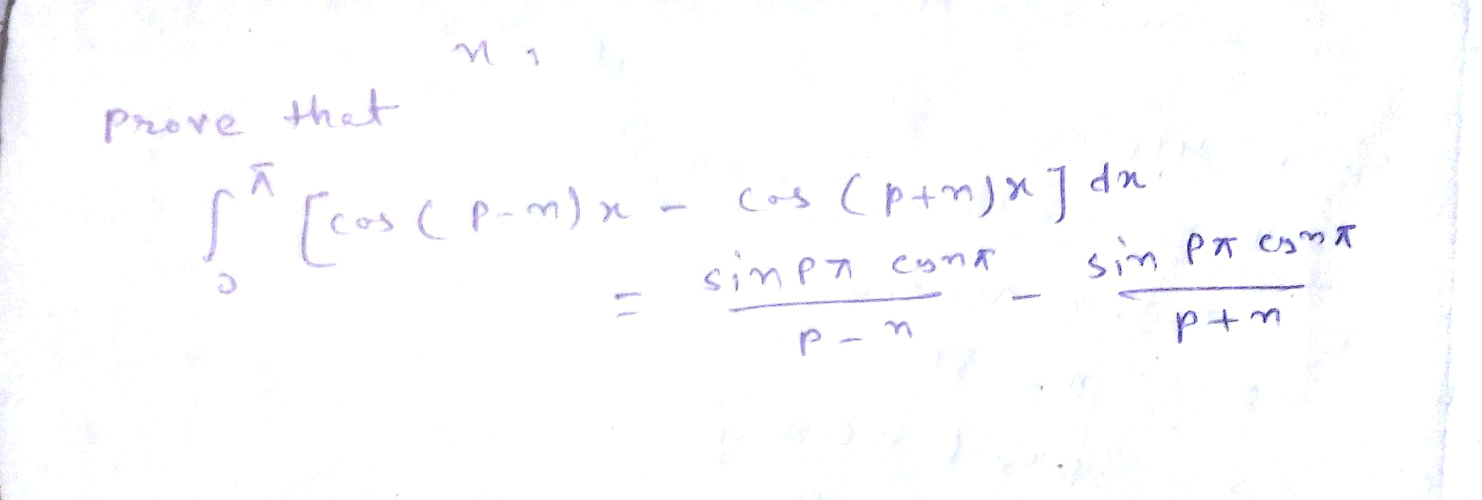
Question Number 25975 Answers: 1 Comments: 0

Question Number 25974 Answers: 0 Comments: 0
Question Number 25973 Answers: 1 Comments: 0
Question Number 25972 Answers: 2 Comments: 0

Question Number 25971 Answers: 1 Comments: 2
Question Number 25969 Answers: 0 Comments: 1
Question Number 25981 Answers: 1 Comments: 0
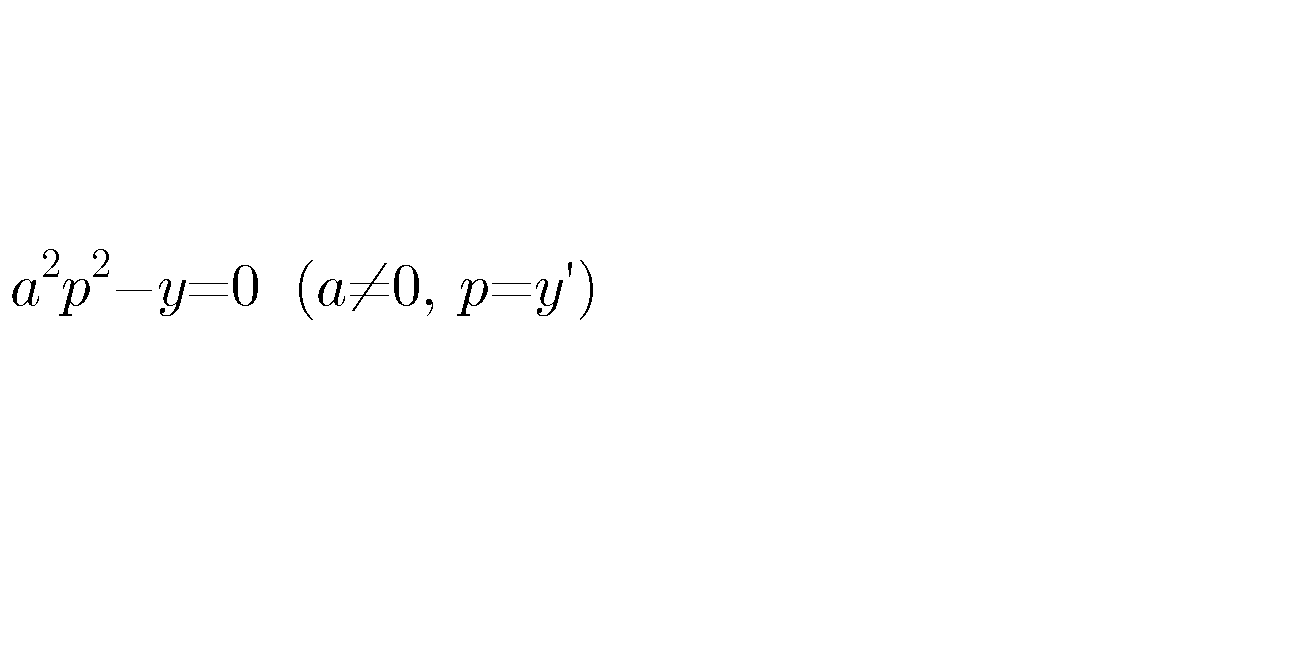
Question Number 25965 Answers: 1 Comments: 0
$${solve}\:{the}\:{integral} \\ $$$$\int\mathrm{sin}^{\mathrm{4}} \theta{d}\theta \\ $$
Question Number 25963 Answers: 0 Comments: 0
Pg 1841 Pg 1842 Pg 1843 Pg 1844 Pg 1845 Pg 1846 Pg 1847 Pg 1848 Pg 1849 Pg 1850
