
AllQuestion and Answers: Page 1835
Question Number 27168 Answers: 0 Comments: 4

Question Number 27159 Answers: 0 Comments: 0
Question Number 27144 Answers: 1 Comments: 1
Question Number 27128 Answers: 1 Comments: 0
Question Number 27117 Answers: 1 Comments: 0

Question Number 27112 Answers: 0 Comments: 2
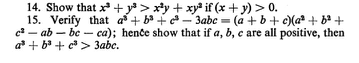
Question Number 27104 Answers: 0 Comments: 1
Question Number 27103 Answers: 0 Comments: 1
Question Number 27102 Answers: 1 Comments: 0

Question Number 27101 Answers: 1 Comments: 0

Question Number 27111 Answers: 1 Comments: 0

Question Number 27098 Answers: 0 Comments: 2
Question Number 27097 Answers: 1 Comments: 2
Question Number 27094 Answers: 1 Comments: 2
Question Number 27083 Answers: 1 Comments: 0
$$\int\mathrm{3}{x}^{\mathrm{2}} /{x}^{\mathrm{6}} +\mathrm{1} \\ $$$$ \\ $$
Question Number 27081 Answers: 1 Comments: 0
Question Number 27076 Answers: 0 Comments: 1
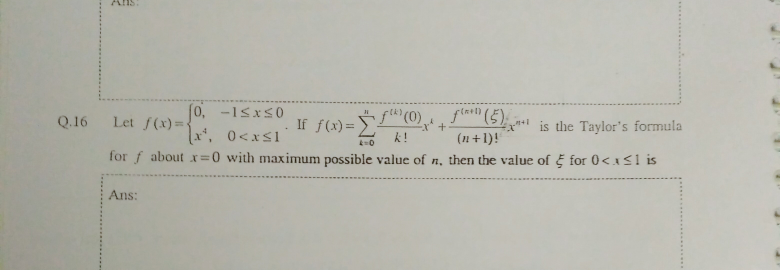
Question Number 27073 Answers: 1 Comments: 0
$$\int\mathrm{ln}\:{x}×\mathrm{cos}\:\mathrm{2ln}\:{xdx} \\ $$
Question Number 27075 Answers: 0 Comments: 0
Question Number 27074 Answers: 2 Comments: 0

Question Number 27065 Answers: 0 Comments: 0

Question Number 27057 Answers: 1 Comments: 3
Question Number 27055 Answers: 1 Comments: 1

Question Number 27050 Answers: 0 Comments: 2

Question Number 27059 Answers: 0 Comments: 2

Question Number 27046 Answers: 0 Comments: 0
Pg 1830 Pg 1831 Pg 1832 Pg 1833 Pg 1834 Pg 1835 Pg 1836 Pg 1837 Pg 1838 Pg 1839
