
AllQuestion and Answers: Page 1834
Question Number 27281 Answers: 1 Comments: 1
Question Number 27280 Answers: 1 Comments: 1
Question Number 27274 Answers: 0 Comments: 0

Question Number 27271 Answers: 1 Comments: 0
Question Number 27270 Answers: 0 Comments: 0
Question Number 27266 Answers: 1 Comments: 0
Question Number 27258 Answers: 0 Comments: 1
Question Number 27254 Answers: 1 Comments: 0

Question Number 27253 Answers: 0 Comments: 0

Question Number 27235 Answers: 1 Comments: 0
Question Number 27224 Answers: 1 Comments: 4

Question Number 27215 Answers: 1 Comments: 0
Question Number 27213 Answers: 1 Comments: 1
Question Number 27204 Answers: 1 Comments: 0
Question Number 27198 Answers: 1 Comments: 0

Question Number 27197 Answers: 1 Comments: 1

Question Number 27203 Answers: 2 Comments: 0
Question Number 27202 Answers: 1 Comments: 0
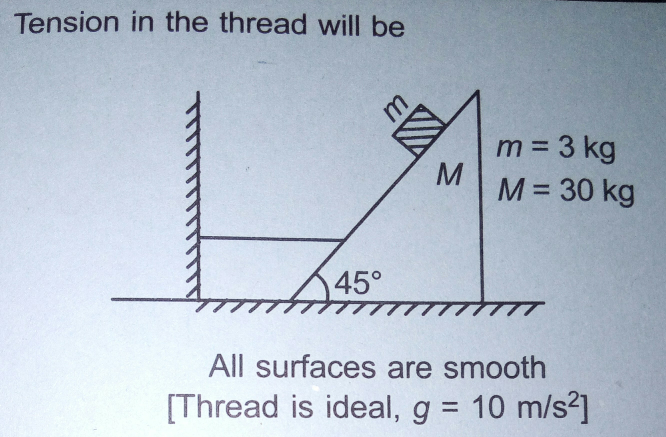
Question Number 27527 Answers: 0 Comments: 1
Question Number 27526 Answers: 1 Comments: 0
Question Number 27189 Answers: 1 Comments: 0
Question Number 27187 Answers: 0 Comments: 1
$${find}\:{I}=\:\:\int_{\mathrm{0}} ^{\propto} \:\frac{{cosx}}{{cosh}\left({x}\right)}{dx} \\ $$
Question Number 27186 Answers: 1 Comments: 1
$${find}\:{I}=\int_{\mathrm{0}} ^{\pi} \:\:\frac{{dx}}{{cosx}\:+\mathrm{2}{sinx}}\:. \\ $$
Question Number 27185 Answers: 0 Comments: 0
Question Number 27184 Answers: 0 Comments: 1
Question Number 27183 Answers: 1 Comments: 0
Pg 1829 Pg 1830 Pg 1831 Pg 1832 Pg 1833 Pg 1834 Pg 1835 Pg 1836 Pg 1837 Pg 1838
