
AllQuestion and Answers: Page 1833
Question Number 27335 Answers: 0 Comments: 1
Question Number 27334 Answers: 1 Comments: 0
Question Number 27332 Answers: 1 Comments: 1
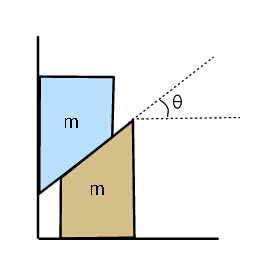
Question Number 27328 Answers: 0 Comments: 1

Question Number 27327 Answers: 0 Comments: 4
Question Number 27326 Answers: 1 Comments: 0
Question Number 27321 Answers: 1 Comments: 1

Question Number 27751 Answers: 0 Comments: 0
Question Number 27309 Answers: 1 Comments: 0
Question Number 27303 Answers: 1 Comments: 0

Question Number 27300 Answers: 3 Comments: 1

Question Number 27296 Answers: 1 Comments: 1
Question Number 27295 Answers: 0 Comments: 1
Question Number 27294 Answers: 0 Comments: 1
Question Number 27293 Answers: 1 Comments: 0
$${L}^{−\mathrm{1}} \left(\frac{{s}^{\mathrm{3}} }{{s}^{\mathrm{4}} +\mathrm{4}}\right)=? \\ $$
Question Number 27287 Answers: 0 Comments: 1

Question Number 27283 Answers: 0 Comments: 0

Question Number 27282 Answers: 0 Comments: 1
$$\int{log}\left(\mathrm{2}+{x}^{\mathrm{2}} \right){dx} \\ $$
Question Number 27281 Answers: 1 Comments: 1
Question Number 27280 Answers: 1 Comments: 1
Question Number 27274 Answers: 0 Comments: 0

Question Number 27271 Answers: 1 Comments: 0
Question Number 27270 Answers: 0 Comments: 0
Question Number 27266 Answers: 1 Comments: 0
Question Number 27258 Answers: 0 Comments: 1
Question Number 27254 Answers: 1 Comments: 0

Pg 1828 Pg 1829 Pg 1830 Pg 1831 Pg 1832 Pg 1833 Pg 1834 Pg 1835 Pg 1836 Pg 1837
